Represent K^N as the sum of exactly N numbers
Last Updated :
24 Nov, 2021
Given two numbers N and K, the task is to represent KN as the sum of exactly N numbers. Print NA if no such numbers are possible.
Examples:
Input: N = 5, K = 2
Output: 2 2 4 8 16
Explanation:
2 + 2 + 4 + 8 + 16 = 32 = 25
Input: N = 4, K = 3
Output: 3 6 18 54
Explanation:
3 + 6 + 18 + 54 = 81 = 34
Approach: In order to obtain numbers such that their sum is a power of K, we can choose the numbers that follow the condition:
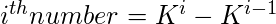
This will always give the sum as a power of K.
For example: This can be illustrated as:
Let N = 3 and K = 4.
We need to represent 43 (=64)
as the sum of exactly 3 numbers
According to the mentioned approach,
The 3 numbers which can be chosen are
(41) = 4
(42 - 41) = 16 - 4 = 12
(43 - 42) = 64 - 16 = 48
Adding the numbers = 4 + 12 + 48 = 64
which is clearly 43
Therefore the required 3 numbers
are 4, 12 and 48.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define ll long long int
using namespace std;
void print(ll n, ll k)
{
cout << k << " ";
for (int i = 2; i <= n; i++) {
ll x = pow(k, i) - pow(k, i - 1);
cout << x << " ";
}
}
int main()
{
ll N = 3, K = 4;
print(N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void print(int n, int k)
{
System.out.print(k+ " ");
for (int i = 2; i <= n; i++) {
int x = (int) (Math.pow(k, i) - Math.pow(k, i - 1));
System.out.print(x+ " ");
}
}
public static void main(String[] args)
{
int N = 3, K = 4;
print(N, K);
}
}
|
Python 3
from math import pow
def printf(n, k):
print(int(k),end = " ")
for i in range(2, n + 1, 1):
x = pow(k, i) - pow(k, i - 1)
print(int(x),end= " ")
if __name__ == '__main__':
N = 3
K = 4
printf(N, K)
|
C#
using System;
class GFG{
static void print(int n, int k)
{
Console.Write(k+ " ");
for (int i = 2; i <= n; i++) {
int x = (int) (Math.Pow(k, i) - Math.Pow(k, i - 1));
Console.Write(x+ " ");
}
}
public static void Main(String[] args)
{
int N = 3, K = 4;
print(N, K);
}
}
|
Javascript
<script>
function print(n, k)
{
document.write( k + " ");
for (var i = 2; i <= n; i++) {
var x = Math.pow(k, i) - Math.pow(k, i - 1);
document.write( x + " ");
}
}
var N = 3, K = 4;
print(N, K);
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...