Represent a number as a sum of maximum possible number of Prime Numbers
Last Updated :
03 May, 2021
Given a positive integer 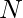 . The task is to represent it as a sum of the maximum possible number of prime numbers. (N > 1)
. The task is to represent it as a sum of the maximum possible number of prime numbers. (N > 1)
Examples:
Input : N = 5
Output : 2 3
Input : N = 6
Output : 2 2 2
At first, the problem might seem to involve some use of Goldbach’s conjecture. But the key observation here is to maximise the number of terms used, you should use as small numbers as possible. This leads to the following idea:
- If N is even, it can be represented as sum of
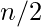 two’s.
two’s. - Otherwise,
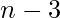 has to be even and hence N can be represented as sum of one 3 and
has to be even and hence N can be represented as sum of one 3 and 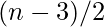 two’s.
two’s.
This is the maximum number of primes whose sum is N.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printAsMaximalPrimeSum(int n)
{
if (n % 2 == 1) {
cout << "3 ";
n -= 3;
}
while (n) {
cout << "2 ";
n -= 2;
}
}
int main()
{
int n = 5;
printAsMaximalPrimeSum(n);
}
|
Java
import java.io.*;
class GFG {
static void printAsMaximalPrimeSum(int n)
{
if (n % 2 == 1) {
System.out.print( "3 ");
n -= 3;
}
while (n>0) {
System.out.print( "2 ");
n -= 2;
}
}
public static void main (String[] args) {
int n = 5;
printAsMaximalPrimeSum(n);
}
}
|
Python3
def printAsMaximalPrimeSum( n):
if ( n % 2 == 1):
print("3 ",end="")
n -= 3
while ( n>0):
print("2 ",end="")
n -= 2
n = 5
printAsMaximalPrimeSum( n)
|
C#
using System;
class GFG
{
static void printAsMaximalPrimeSum(int n)
{
if (n % 2 == 1) {
Console.Write("3 ");
n -= 3;
}
while (n>0) {
Console.Write("2 ");
n -= 2;
}
}
public static void Main()
{
int n = 5;
printAsMaximalPrimeSum(n);
}
}
|
PHP
<?php
function printAsMaximalPrimeSum($n)
{
if ($n % 2 == 1) {
echo "3 ";
$n -= 3;
}
while ($n>0) {
echo "2 ";
$n -= 2;
}
}
$n = 5;
printAsMaximalPrimeSum($n);
?>
|
Javascript
<script>
function printAsMaximalPrimeSum(n)
{
if (n % 2 == 1) {
document.write( "3 ");
n -= 3;
}
while (n>0) {
document.write( "2 ");
n -= 2;
}
}
let n = 5;
printAsMaximalPrimeSum(n);
</script>
|
Time Complexity: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...