Refraction of Light through Glass Slab
Last Updated :
19 Apr, 2021
Glass slab is a substance or sheet made of a glass material having 3 dimensions that is length breadth and height, it is cuboidal shaped. It does not deviate nor does it disperse the light rays passing through it. This means that the incident and the emergent ray emerging from the glass slab are parallel. The glass slab only and only produces a lateral or (sideways) shift or displacement to the direction of light.
As we can observe and see below, the refraction or bending of light rays through a glass slab takes place at the two parallel and equal and opposite surfaces. As we can see and observe the incident ray which falls on one of the parallel surfaces of the slab first undergoes refraction at the PS surface and the refracted ray bends towards the normal, and again it is incident on the other surface which is equal to the first one and that is QR. Through a glass slab, the light before coming back to the air suffers refraction two times. At the second time, the refracted ray bends away from the normal. If the light is incident at right angles then it will pass through the glass slab without any deviation. The emergent ray as we can see has emerged parallel to the before an incident ray of light. This is a characteristic property of a glass slab as it has two opposite and parallel equal faces from which the rays emerge.
Now we can easily trace the ray of light after passing through glass slab as follows:

Related Terms
Incident Ray- The ray of light falling obliquely on one of the surfaces of the glass slab is known or referred to as the incident ray. We can use many light sources to generate incident rays for observing the refraction occurring through a glass slab.
Refracted Ray- The ray of light that emerges after refraction through one of the surfaces on which the incident ray has struck. The refracted ray moves toward normal in case the light enters from rarer medium to denser, or it moves further away from the normal ray in case the light travels from denser to rarer medium.
Normal Ray- Two normal rays are drawn at the two opposite parallel surfaces of the slab from where we measure the angles of incidence, refraction, and emergence respectively.
Emergent Ray- The ray of light which emerges from another opposite face of the glass slab is called the emergent ray. It has been seen or observed that emergent ray emerges somewhat parallel to the path from where incident ray could have emerged if it would not have experienced any change.
Lateral Displacement
There is a distance between the incident and the emergent ray that emerged. This distance is known as lateral displacement or shift. We consider it a shift from the original path from where the incident ray of light was supposed to emerge if it would not have experienced or undergone any refraction. The thicker the glass slab is the more shift or displacement from the original incident position is observed.
It depends upon the thickness of the given glass slab and on the angle of incidence and refraction respectively. The formula of lateral displacement is given below:

Where i = angle of incidence
r = angle of refraction
t = thickness of the given glass slab
l = lateral displacement or shift
Laws of Refraction
Based on the refraction through different surfaces, some common properties were observed in all. There are given two laws of refraction as given and stated below which at the sight of refraction the light follows and what we see is the refracted image formed of the object.
- The refracted ray from the surface, incident or what we call obliquely falling ray, and the normal ray at the point of incidence all will tend to lie together in the same plane.
- We have the ratio of sin of angle of the incidence and refraction is a constant or has definite value. Which is stated as Snell’s law.
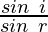 =constant
=constant- Where we have i = angle of incidence, r = angle of refraction, the constant value which depends upon the refractive indexes of the two taken mediums. It is their ratio and is dimensionless.
Sample Problems
Question 1: What is the constant value if the angle of refraction is given to be 15° and the angle of incidence is 35°?
Solution:
As we know,
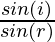 =constant
=constant
Given sin i = sin35° and sin r = sin15°
Putting the respective values of the given angles from log table we get
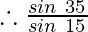 = 2.19
= 2.19
Hence, the constant for the above-given values is 2.19.
Question 2: What is the value of the sin of angle of incidence if the angle of refraction is given to be 35°? The constant is assumed to be 1.57.
Solution:
As we know,
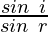 = constant
= constant
Given constant has value = 1.57 and sin r = 35° = 0.57
Putting the respective values of the angles from log table we get
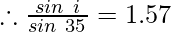
sin i = 1.57 × 0.57
{sin i} = 0.894
Hence, sin of the angle of incidence or sin i = 0.894.
Question 3:What is the constant value if the angle of incidence is 45° and the angle of refraction is given to be 60°?
Solution:
As we know,
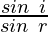 = constant
= constant
Given sin i = sin 45° and sin r = sin 60°
Putting the respective values of the given angles from log table we get
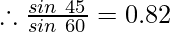
Hence, the value of the constant is found to be 0.82.
Question 4: What will happen to the emergent ray that will come from the surface of glass slab if the angle of incidence is perpendicular or along the normal ray?
Answer:
The emergent will be along the normal itself as the incident ray will not suffer any refraction as it strikes along the normal ray at the surface of the glass slab.
Question 5: Does the light ray that travels from the surface of the glass slab undergo any dispersion or deviation?
Answer:
No, the light ray that travels through the glass slab doesn’t face any dispersion or any deviation as because the surfaces of glass slab are equal and opposite to each other hence no deviation or dispersion phenomenon occur.
Question 6: By applying the lateral displacement formula find out the lateral displacement through a glass slab which has a thickness of 5cm and the angle of incidence is 45° and refraction is 30°.
Solution:
From the given formula of lateral displacement we have,
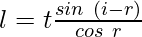
Given t = 5 cm, ∠i = 45° and ∠r = 30°
Therefore, putting the values in the above equation we have,
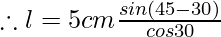
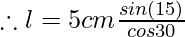
Putting respective angle values from log table we get,
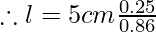

l = 1.45 cm
Therefore, the shift or lateral displacement is 1.45cm.
Question 7: By applying the lateral displacement formula find out the lateral displacement through a glass slab which has a thickness of 10 cm and the angle of incidence is 60° and refraction is 45°.
Solution:
From the given formula of lateral displacement we have,

Given t = 10 cm, ∠i = 60° and ∠r = 45°
Therefore putting the values in the above equation we have,
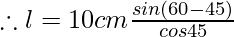
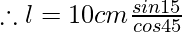
Putting respective angle values from log table we get,
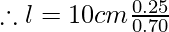
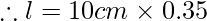
l = 3.5 cm
Therefore, the shift or lateral displacement is 3.5cm.
Question 8: By applying the lateral displacement formula find out the thickness of a given glass slab which has a shift or lateral displacement of 5 cm and the angle of incidence is 45° and refraction is 30°.
Solution:
From the formula of lateral displacement we have,

Given l = 5 cm ∠i = 45° and ∠r = 30°
Therefore putting the values in the above equation we have,
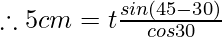
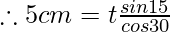
Putting respective angle values from log table we get,

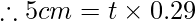

Therefore, the thickness of given slab is 17.24cm.
Share your thoughts in the comments
Please Login to comment...