Rat and Poisoned bottle Problem

Given N number of bottles in which one bottle is poisoned. So the task is to find out minimum number of rats required to identify the poisoned bottle. A rat can drink any number of bottles at a time. 

Examples:

Input: N = 4 
Output: 2

Input: N = 100
Output: 7

Approach:
Let’s start from the base case. 

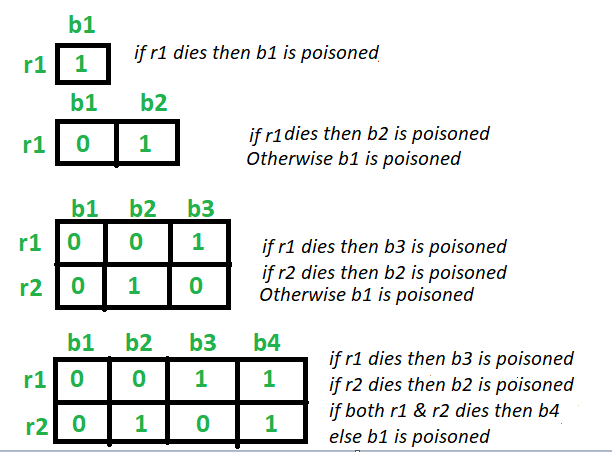
• For 2 bottles: Taking one rat (R1). If the rat R1 drinks the bottle 1 and dies, then bottle 1 is poisonous. Else the bottle 2 is poisonous. Hence 1 rat is enough to identify
• For 3 bottles: Taking two rats (R1) and (R2). If the rat R1 drinks the bottle 1 and bottle 3 and dies, then bottle 1 or bottle 3 is poisonous. So the rat R2 drinks the bottle 1 then. If it dies, then the bottle 1 is poisonous, Else the bottle 3 is poisonous. 
  Now if the rat R1 does not die after drinking from bottle 1 and bottle 3, then bottle 2 is poisonous. 
  Hence 2 rats are enough to identify. 
  
• For 4 bottles: Taking two rats (R1) and (R2). If the rat R1 drinks the bottle 1 and bottle 3 and dies, then bottle 1 or bottle 3 is poisonous. So the rat R2 drinks the bottle 1 then. If it dies, then the bottle 1 is poisonous, Else the bottle 3 is poisonous. 
  Now if the rat R1 does not die after drinking from bottle 1 and bottle 3, then bottle 2 or bottle 4 is poisonous. So the rat R1 drinks the bottle 2 then. If it dies, then the bottle 2 is poisonous, Else the bottle 4 is poisonous. 
  Hence 2 rats are enough to identify. 
  
• For N bottles:

Minimum number of rats required are = ceil(log₂ N))

Below is the implementation of the above approach:  

C++

// C++ program to implement
// the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the minimum number of rats
int minRats(int n)
{
    return ceil(log2(n));
}

// Driver Code
int main()
{
    // Number of bottles
    int n = 1025;

    cout << "Minimum " << minRats(n)
         << " rat(s) are required"
         << endl;

    return 0;
}

Java

// Java program to implement
// the above approach
class GFG
{
    public static double log2(int x)
    {
        return (Math.log(x) / Math.log(2));
    }

    // Function to find the minimum number of rats
    static int minRats(int n)
    {
        return (int)(Math.floor(log2(n)) + 1);
    }

    // Driver Code
    public static void main (String[] args)
    {
        // Number of bottles
        int n = 1025;

        System.out.println("Minimum " + minRats(n) +
                           " rat(s) are required");
    }
}

// This code is contributed by AnkitRai01

Python3

# Python3 program to implement
# the above approach
import math

# Function to find the
# minimum number of rats
def minRats(n):

    return math.ceil(math.log2(n));

# Driver Code

# Number of bottles
n = 1025;
print("Minimum ", end = "")
print(minRats(n), end = " ")
print("rat(s) are required")

# This code is contributed
# by divyamohan123

C#

// C# program to implement
// the above approach
using System;

class GFG
{
    public static double log2(int x)
    {
        return (Math.Log(x) / Math.Log(2));
    }

    // Function to find the minimum number of rats
    static int minRats(int n)
    {
        return (int)(Math.Floor(log2(n)) + 1);
    }

    // Driver Code
    public static void Main (String[] args)
    {
        // Number of bottles
        int n = 1025;

        Console.WriteLine("Minimum " + minRats(n) +
                          " rat(s) are required");
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript program to implement
// the above approach

// Function to find the minimum number of rats
function minRats(n)
{
    return Math.ceil(Math.log2(n));
}

// Driver Code

// Number of bottles
var n = 1025;
document.write("Minimum " + minRats(n) +
               " rat(s) are required");

// This code is contributed by importantly

</script>

Output:

Minimum 11 rat(s) are required