Random Numbers Ecosystem in Julia – The Natural Side
Last Updated :
16 Aug, 2021
If we keenly observe, randomness can be effectively derived from nature. Despite being explainable by scientific phenomena, the behavior of most matter on earth is random(though it may depend on the conditions around). Eg: The fluttering of leaves on a tree though justifiable by physics, is random to the human eye, the movement of players on a football field is again quite random though influenced by strategy/position of the ball, etc.
In the last article, we talked about the mathematical/algorithmic approach towards random number generation, hence pseudo. Pseudo random number generators are quiet good for general applications. But they have once shortcoming. If a third person is aware of the seed value that the RNG is initialized with, he/she can easily predict the sequence of numbers that might be given out by the RNG. This can cause a serious lapse in the application stages.
True Random Number Generators(TRNGs)
To fix this problem, one way out is using the TRNGs(True Random Number Generators) instead of PRNGs.
But the generation of TRNGs tend to be very slow, and the user might have to wait before getting the desired number of random values. Also their performance/effectiveness depends very much on the source. eg: The initial value might not be predictable but we might end up with a consistent pattern/stream of random numbers.
Other way is to seed the PRNG with a value generated by the TRNG. This way our seed value, hence the final output tends to become more secure since the seed value too is random. There are many TRNG sources available. One of the most random sources is the atmospheric noise caused to to thundering, space debris etc. This approach is quite effecting and mostly used.
Tunneling nature’s randomness into computers
Generating random numbers from the nature is a classical yet effective approach. Random.org is an organisation that generates randomness from atmospheric noise. You can check the above link and use the services they offer. But what if we are running a simulation that needs autonomous and continuous input of random numbers at a particular step? We just can’t go to the random.org website every time and copy the numbers. Fortunately Random.org offers an API, that allows developers to write clients for their interface. The API client will then directly make an HTTP call to the Random.org servers and fetch the required data.
TRNGs in Julia
Coming to Julia, there is provision to exploit JSON-RPC requests and HTTP calls(though the HTTP.jl and JSON.jl respectively). But manually making POST requests, everytime we need random numbers might become tiresome. Fortunately the Randomorg_API.jl packages handles this for us. The link to the package with a detailed readme is available here.
Currently the package supports the following functions:
generateIntegers() Function
This method generates true random integers within a user-defined range.
Syntax:
generateIntegers(n, min, max, replacement)
Parameters:
- n: It specifies how many random integers you need.
- min: It is the lower boundary for the range from which the random numbers will be picked.
- max: It is the upper boundary for the range from which the random numbers will be picked.
- replacement: It specifies whether the random numbers should be picked with replacement. The default (true) will cause the numbers to be picked with replacement, i.e., the resulting numbers may contain duplicate values. If you want the numbers picked to be unique, set this value to false.
Example:
Python3
using Randomorg_API
generateIntegers(4, 1, 1000, true)
|
Output:

generateIntegerSequences() Function
This method generates uniform or multiform sequences of true random integers within user-defined range.
Syntax:
generateIntegerSequences(n, length, min, max, replacement)
Example:
Python3
generateIntegerSequences(2, 4, -100, 100, true)
|
Output:

generateDecimalFractions() Function
This method generates true random decimal fractions from a uniform distribution across
the [0, 1] interval with a user-defined number of decimal places.
Syntax:
generateDecimalFractions(n, decimalPlaces, replacement)
Parameters:
decimalPlaces: The number of decimal places to use.
Example:
Python3
generateDecimalFractions(4, 3, true)
|
Output:

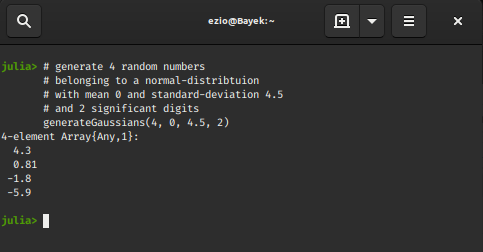
generateGaussians() Function
This method generates true random numbers from a Gaussian distribution (also known as
a normal distribution).
Syntax:
generateGaussians(n, mean, standardDeviation, significantDigits)
Parameters:
- mean The distribution’s mean.
- standardDeviation The distribution’s standard deviation.
The form uses a Box-Muller Transform to generate the Gaussian distribution from uniformly distributed numbers.
Example:
Python3
generateGaussians(4, 0, 4.5, 2)
|
Output:
generateStrings() Function
This method generates true random strings.
Syntax:
generateStrings(n, length, characters, replacement)
Parameters:
- characters: A string that contains the set of characters that are allowed to occur in the random strings.
- length: The length of each string.
Example:
Python3
generateStrings(4, 4, "abcdefghij", false)
|
Output:

generateUUIDs() Function
This method generates version 4 true random Universally Unique Identifiers(UUIDs)
Syntax:
generateUUIDs(n)
Example:
Output:

generateBlobs() Function
This method generates Binary Large Objects(BLOBs) containing true random data.
Syntax:
generateBlobs(n, size, format)
Example:
Python3
generateBlobs(4, 56, "base64")
|
Output:

There are many such services online, eg: the HotBits service of FermiLab uses radioactivity, world renowned Cloudflare uses a large number of lava-lamps and image-processing for random number generation.
From the previous article you might recall, we talked about the hardware based random number generator on Intel chips, viz. RDRAND. One might wonder if we can directly communicate with RDRAND to get processor generated entropy. In Julia we exploit this method with this package. It is a nicely written module and you might consider trying it out.
Share your thoughts in the comments
Please Login to comment...