Queries for decimal values of subarrays of a binary array

Given a binary array arr[], we to find the number represented by the subarray a[l..r]. There are multiple such queries.

Examples:

Input :  arr[] = {1, 0, 1, 0, 1, 1};
         l = 2, r = 4
         l = 4, r = 5
Output : 5
         3 
Subarray 2 to 4 is 101 which is 5 in decimal.
Subarray 4 to 5 is 11 which is 3 in decimal.

Input : arr[] = {1, 1, 1}
        l = 0, r = 2
        l = 1, r = 2
Output : 7
         3

A Simple Solution is to compute decimal value for every given range using simple binary to decimal conversion. Here each query takes O(len) time where len is length of range.

An Efficient Solution is to do per-computations, so that queries can be answered in O(1) time. 

The number represented by subarray arr[l..r] is arr[l]*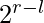+ arr[l+1]*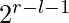….. + arr[r]*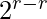

1. Make an array pre[] of same size as of given array where pre[i] stores the sum of arr[j]*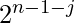where j includes each value from i to n-1.
2. The number represented by subarray arr[l..r] will be equal to (pre[l] – pre[r+1])/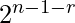.pre[l] – pre[r+1] is equal to arr[l]*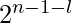+ arr[l+1]*+……arr[r]*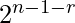. So if we divide it by 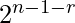, we get the required answer

Flowchart

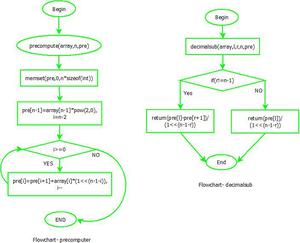
Flowchart

Implementation:

C++

// C++ implementation of finding number
// represented by binary subarray
#include <bits/stdc++.h>
using namespace std;

// Fills pre[]
void precompute(int arr[], int n, int pre[])
{
    memset(pre, 0, n * sizeof(int));
    pre[n - 1] = arr[n - 1] * pow(2, 0);
    for (int i = n - 2; i >= 0; i--)
        pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
}

// returns the number represented by a binary
// subarray l to r
int decimalOfSubarr(int arr[], int l, int r,
                    int n, int pre[])
{
    // if r is equal to n-1 r+1 does not exist
    if (r != n - 1)
        return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));

    return pre[l] / (1 << (n - 1 - r));
}

// Driver Function
int main()
{
    int arr[] = { 1, 0, 1, 0, 1, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);

    int pre[n];
    precompute(arr, n, pre);
    cout << decimalOfSubarr(arr, 2, 4, n, pre) << endl;
    cout << decimalOfSubarr(arr, 4, 5, n, pre) << endl;
    return 0;
}

Java

// Java implementation of finding number
// represented by binary subarray
import java.util.Arrays;

class GFG {

    // Fills pre[]
    static void precompute(int arr[], int n, int pre[])
    {
        Arrays.fill(pre, 0);

        pre[n - 1] = arr[n - 1] * (int)(Math.pow(2, 0));
        for (int i = n - 2; i >= 0; i--)
            pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
    }

    // returns the number represented by a binary
    // subarray l to r
    static int decimalOfSubarr(int arr[], int l, int r,
                               int n, int pre[])
    {

        // if r is equal to n-1 r+1 does not exist
        if (r != n - 1)
            return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));

        return pre[l] / (1 << (n - 1 - r));
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 1, 0, 1, 0, 1, 1 };
        int n = arr.length;

        int pre[] = new int[n];
        precompute(arr, n, pre);

        System.out.println(decimalOfSubarr(arr,
                                           2, 4, n, pre));

        System.out.println(decimalOfSubarr(arr,
                                           4, 5, n, pre));
    }
}

// This code is contributed by Anant Agarwal.

Python3

# implementation of finding number
# represented by binary subarray
from math import pow

# Fills pre[]
def precompute(arr, n, pre):

    pre[n - 1] = arr[n - 1] * pow(2, 0)
    i = n - 2
    while(i >= 0):
        pre[i] = (pre[i + 1] + arr[i] *
                 (1 << (n - 1 - i)))
        i -= 1

# returns the number represented by
# a binary subarray l to r
def decimalOfSubarr(arr, l, r, n, pre):

    # if r is equal to n-1 r+1 does not exist
    if (r != n - 1):
        return ((pre[l] - pre[r + 1]) /
                (1 << (n - 1 - r)))

    return pre[l] / (1 << (n - 1 - r))

# Driver Code
if __name__ == '__main__':
    arr = [1, 0, 1, 0, 1, 1]
    n = len(arr)

    pre = [0 for i in range(n)]
    precompute(arr, n, pre)
    print(int(decimalOfSubarr(arr, 2, 4, n, pre)))
    print(int(decimalOfSubarr(arr, 4, 5, n, pre)))

# This code is contributed by
# Surendra_Gangwar

C#

// C# implementation of finding number
// represented by binary subarray
using System;

class GFG {

    // Fills pre[]
    static void precompute(int[] arr, int n, int[] pre)
    {
        for (int i = 0; i < n; i++)
            pre[i] = 0;

        pre[n - 1] = arr[n - 1] * (int)(Math.Pow(2, 0));
        for (int i = n - 2; i >= 0; i--)
            pre[i] = pre[i + 1] + arr[i] * (1 << (n - 1 - i));
    }

    // returns the number represented by
    // a binary subarray l to r
    static int decimalOfSubarr(int[] arr, int l, int r,
                                      int n, int[] pre)
    {
        // if r is equal to n-1 r+1 does not exist
        if (r != n - 1)
            return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));

        return pre[l] / (1 << (n - 1 - r));
    }

    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 0, 1, 0, 1, 1 };
        int n = arr.Length;

        int[] pre = new int[n];
        precompute(arr, n, pre);

        Console.WriteLine(decimalOfSubarr(arr,
                                        2, 4, n, pre));

        Console.WriteLine(decimalOfSubarr(arr,
                                        4, 5, n, pre));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP implementation of finding number
// represented by binary subarray

// Fills pre[]
function precompute(&$arr, $n, &$pre)
{
    $pre[$n - 1] = $arr[$n - 1] * pow(2, 0);
    for ($i = $n - 2; $i >= 0; $i--)
        $pre[$i] = $pre[$i + 1] + $arr[$i] *
                           (1 << ($n - 1 - $i));
}

// returns the number represented by
// a binary subarray l to r
function decimalOfSubarr(&$arr, $l, $r, $n, &$pre)
{
    // if r is equal to n-1 r+1 does not exist
    if ($r != $n - 1)
        return ($pre[$l] - $pre[$r + 1]) /
                    (1 << ($n - 1 - $r));

    return $pre[$l] / (1 << ($n - 1 - $r));
}

// Driver Code
$arr = array(1, 0, 1, 0, 1, 1 );
$n = sizeof($arr);

$pre = array_fill(0, $n, NULL);
precompute($arr, $n, $pre);
echo decimalOfSubarr($arr, 2, 4, $n, $pre) . "\n";
echo decimalOfSubarr($arr, 4, 5, $n, $pre) . "\n";

// This code is contributed by ita_c
?>

Javascript

<script>

// Javascript implementation of finding number
// represented by binary subarray


// Fills pre[]
function precompute(arr, n, pre)
{
    for (let i = 0; i < n; i++)
        pre[i] = 0;

    pre[n - 1] = arr[n - 1] * (Math.pow(2, 0));
    for (let i = n - 2; i >= 0; i--)
        pre[i] = pre[i + 1] + arr[i] *
                 (1 << (n - 1 - i));
}

// returns the number represented by
// a binary subarray l to r
function decimalOfSubarr(arr, l, r,n, pre)
{
    // if r is equal to n-1 r+1 does not exist
    if (r != n - 1)
        return (pre[l] - pre[r + 1]) / (1 << (n - 1 - r));

    return pre[l] / (1 << (n - 1 - r));
}

// Driver code

let arr = [1, 0, 1, 0, 1, 1];
let n = arr.length;

let pre = new Array(n)
precompute(arr, n, pre);

document.write(decimalOfSubarr(arr,2, 4, n, pre)+"<br>");

document.write(decimalOfSubarr(arr, 4, 5, n, pre));

</script>

Output

5
3

Time complexity: O(n)
Auxiliary Space: O(n)

This article is contributed by Ayush Jha. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.