Python Set | symmetric_difference()
Last Updated :
15 Sep, 2023
Python Set symmetric_difference() method is used to get the elements present in either of the two sets, but not common to both sets. In this article, we are going to learn about the Python Set symmetric_difference() function.
Example
Input: set_A = {1, 2, 3, 4, 5}, set_B = {6, 7, 3, 9, 4}
Output: {1, 2, 5, 6, 7, 9}
Explanation: Output is the set of numbers that are present in either of the sets but not in both the sets.
Python Set | symmetric_difference()
This method is used with sets to find the symmetric difference between two sets. The symmetric difference of two sets A and B is a set of elements that are in either A or B, but not in both.
Syntax of symmetric_difference()
Syntax: set_A.symmetric_difference(set_B)
Parameter: Takes a single parameter that has to be a set
Return: Returns a new set which is the symmetric difference between the two sets.
Pictorial Representation of Python symmetric_difference()
Let’s look at the Venn diagram of the symmetric difference between two sets. The symmetric Difference is marked in Green If there are a set_A and set_B, then the symmetric difference between them will be equal to the union of set_A and set_B without the intersection between the two.
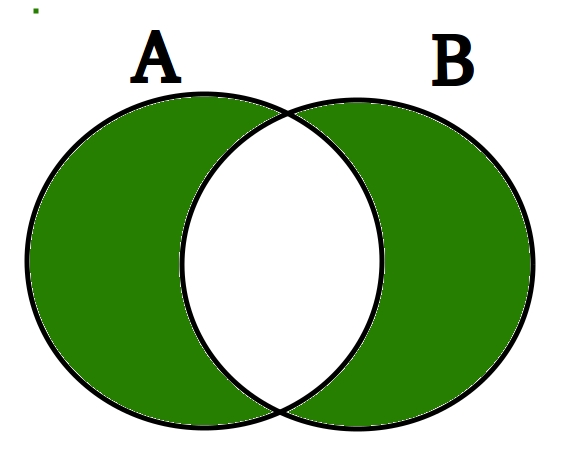
Python Set symmetric_difference() Venn diagram
In this example, we are defining two sets and then by using symmetric_difference() method to find the elements present in either of the sets but not common in both sets.
Python3
set_A = {1, 2, 3, 4, 5}
set_B = {6, 7, 3, 9, 4}
print(set_A.symmetric_difference(set_B))
|
Output
{1, 2, 5, 6, 7, 9}
Python Set symmetric_difference Examples
Below are some examples of how we can implement symmetric_difference on sets, iterable and even use ‘^’ operator to find the symmetric difference between two sets.
Python Set | symmetric_difference()
In the example, the symmetric_difference() method returns a new set containing elements {1, 2, 4, 5}. These elements are present in either set1 or set2, but not in both.
Python3
set1 = {1, 2, 3}
set2 = {3, 4, 5}
result = set1.symmetric_difference(set2)
print(result)
|
symmetric_difference() on a Set and List
In this example, we are using to symmetric_difference() to find the symmetric_difference where we are given a set and a list.
Python3
A = {3,5,9,8}
B = [4,5,2,1]
result = A.symmetric_difference(B)
print(result)
|
Output
{1, 2, 3, 4, 8, 9}
Symmetric Difference Using ^ Operator in Python
We can also find symmetric differences between two sets using the ‘^’ operator in Python.
Python3
set_A = {"ram", "rahim", "ajay", "rishav", "aakash"}
set_B = {"aakash", "ajay", "shyam", "ram", "ravi"}
print(set_A ^ set_B)
|
Output
{'ravi', 'rishav', 'rahim', 'shyam'}
Python Set symmetric_difference() with multiple Sets
In the first section, A.symmetric_difference(B) and B.symmetric_difference(A) are called. These operations compute the symmetric difference between sets A and B, resulting in sets that contain elements present in either A or B, but not in both. The second section involves A.symmetric_difference(C) and B.symmetric_difference(C). Here, the symmetric difference between set A and an empty set C is evaluated, as well as the symmetric difference between set B and C. The former returns a set that includes all elements of A since C is empty, while the latter simply returns B itself because all its elements are absent in C.
Python
A = {'p', 'a', 'w', 'a', 'n'}
B = {'r', 'a', 'o', 'n', 'e'}
C = {}
print(A.symmetric_difference(B))
print(B.symmetric_difference(A))
print(A.symmetric_difference(C))
print(B.symmetric_difference(C))
|
Output
set(['e', 'o', 'p', 'r', 'w'])
set(['e', 'o', 'p', 'r', 'w'])
set(['a', 'p', 'w', 'n'])
set(['a', 'r', 'e', 'o', 'n'])
Share your thoughts in the comments
Please Login to comment...