Python program to find the redundancy rates for each row of a matrix

Given a Matrix, the task is to write a python program that can compute redundancy rates of each row, i.e rate of total number of repeated characters.

Redundancy Rate : Rate of repetition of elements.

Formula:

$1 - (total unique elements) / (total elements)$

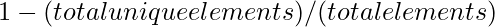
Examples:

Input : test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Output : [0.19999999999999996, 0.8, 0.6, 0.0]
Explanation : 1 – [2/5] = 0.6 for 3rd row.
Input : test_list = [[5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Output : [0.8, 0.6, 0.0]
Explanation : 1 – [2/5] = 0.6 for 2nd row.

Method 1 : Using loop and set()

In this, we perform task of computing rate using fraction of unique elements computed using length of set, to all the elements in list, subtracted from 1.

Example:

Python3

# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5],
             [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
res = []
for sub in test_list:
 
    # getting Redundancy
    res.append(1 - len(set(sub)) / len(sub))
 
# printing result
print("Matrix Redundancy ? : " + str(res))

Output:

The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time Complexity: O(n*m)
Auxiliary Space: O(n)

Method 2 : Using list comprehension

Uses similar functionality as above method, only difference is that its one liner solution computed using list comprehension.

Example:

Python3

# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5],
             [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
# list comprehension for one liner
res = [1 - len(set(sub)) / len(sub) for sub in test_list]
 
# printing result
print("Matrix Redundancy ? : " + str(res))

Output:

The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time Complexity: O(n) where n is the number of elements in the list “test_list”. The list comprehension is used to perform the task and it takes O(n) time.
Auxiliary Space: O(n), new list of size O(n) is created where n is the number of elements in the list

Method #3:Using Counter() function

Python3

from collections import Counter
# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5],
             [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
res = []
for sub in test_list:
 
    # getting Redundancy
    freq = Counter(sub)
    res.append(1 - len(freq) / len(sub))
 
# printing result
print("Matrix Redundancy ? : " + str(res))

Output

The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time Complexity: O(N*N)

Auxiliary Space: O(N)

Method#4: Using Recursive method.

Algorithm:

Define a function named matrix_redundancy that takes a list as an argument.
Check if the input is a non-empty list.
Take the first sublist in the list and calculate its redundancy using the formula: 1 – (number of unique elements in the sublist / total number of elements in the sublist).
Recursively call the matrix_redundancy function for the remaining sublists in the list.
Combine the redundancy of the current sublist with the result of the recursive call and return the combined list.
If the input list is empty or not a list, return an empty list.
Call the matrix_redundancy function with the input list and store the result in a variable.
Print the result.

Python3

def matrix_redundancy(test_list):
    if isinstance(test_list, list) and test_list:
        sub = test_list[0]
        # getting Redundancy
        redundancy = 1 - len(set(sub)) / len(sub)
        # recursive call for remaining elements
        return [redundancy] + matrix_redundancy(test_list[1:])
    else:
        return []
 
# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5],
            [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
res = matrix_redundancy(test_list)
 
# printing result
print("Matrix Redundancy ? : " + str(res))

Output

The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time complexity:

The time complexity of this algorithm is O(n^2), where n is the number of sublists in the input list. This is because the algorithm iterates through each sublist in the list and performs a set operation, which has a time complexity of O(n). Since the algorithm performs this operation for each sublist, the time complexity becomes O(n^2).

Auxiliary Space:

The space complexity of this algorithm is O(n), where n is the number of sublists in the input list. This is because the algorithm creates a list to store the redundancy of each sublist in the input list. Since the list contains n elements, the space complexity becomes O(n).

Method #3: Using map() + lambda function

In this approach, we use the map() function with a lambda function to apply the same logic on each sublist of the original list. The lambda function calculates the redundancy value for each sublist and returns a list of these values.

Below is the code for the above approach.

Python3

from collections import Counter
 
# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
res = list(map(lambda sub: 1 - len(Counter(sub))/len(sub), test_list))
 
# printing result
print("Matrix Redundancy ? : " + str(res))

Output

The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time Complexity: O(n*m), where n is the number of sublists in the test_list and m is the length of the longest sublist.

Auxiliary Space: O(n), as we create a new list res, which has n elements.

Method 6 : using NumPy library.

steps to follow:

Step 1: Import NumPy library
Step 2: Convert the original list into a NumPy array
Step 3: Use NumPy’s unique() function to get the unique elements in each sub-list
Step 4: Divide the length of the original sub-list with the length of the unique sub-lists
Step 5: Subtract the result from 1 to get the redundancy
Step 6: Append the result to a new list
Step 7: Print the final result

Python3

import numpy as np
 
# initializing list
test_list = [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5],
             [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
 
# printing original list
print("The original list is : " + str(test_list))
 
res = []
for sub in test_list:
    # converting sub-list to NumPy array
    sub_arr = np.array(sub)
    # getting unique elements in sub-array
    unique_arr = np.unique(sub_arr)
    # getting redundancy
    redun = 1 - len(unique_arr) / len(sub_arr)
    res.append(redun)
 
# printing result
print("Matrix Redundancy ? : " + str(res))

OUTPUT : 
The original list is : [[4, 5, 2, 4, 3], [5, 5, 5, 5, 5], [8, 7, 8, 8, 7], [1, 2, 3, 4, 5]]
Matrix Redundancy ? : [0.19999999999999996, 0.8, 0.6, 0.0]

Time complexity: The time complexity of this approach is O(n^2) because we are iterating over each sub-list and performing a unique operation which is an O(n) operation.

Auxiliary space: The auxiliary space complexity of this approach is O(n) because we are using a new list to store the result.

Last Updated : 04 May, 2023