Properties of Region of Convergence (ROC) of the Z-Transform

The Z-transform is a mathematical tool used primarily in digital signal processing and discrete-time systems analysis. Our basic introduction for the properties of the region of convergence (ROC) of the Z-Transform starts with the basic question, what do we exactly mean by Region of Convergence. In this article we will be going through the properties of the region of convergence in the Z transform in brief.

What is Z-Transform?

The Z-transform is a mathematical tool used primarily in digital signal processing and discrete-time systems analysis. It’s analogous to the Laplace transform used in continuous-time systems. In discrete-time signal processing, signals are represented as sequences of values sampled at discrete points in time. The Z-transform converts a discrete-time signal, which is a sequence of numbers, into a function of a complex variable Z.

The Z-transform is a useful tool for engineers to examine the stability, frequency response, and transient behaviour of discrete systems. Engineers can create and optimize digital filters, control systems, and other signal-processing techniques by algebraically modifying the Z-transformed functions. It is a vital instrument for today’s digital signal processing because of its wide range of applications in control systems, audio processing, and telecommunications.

What is Region of Convergence (ROC)signal-processing?

It is a set of values in the complex plane that a specific transform converges to. Functions are expressed in terms of complex variables in a number of signal-processing transforms, including the Z-transform and Laplace transform. The range of values for which these transforms converge and are mathematically well-defined is shown by the ROC.

Region of Convergence is defined for two types of Transform

The ROC of Z- Transform- Considering a discrete-time signal or system which is described by the Z-transform is the set of complex values of X(z), the region of convergence, is the sum of series that converges for z for which the Z-transform converges absolutely. In the complex plane, the ROC may be located on, outside, or inside the unit circle.

The Z-transform of a discrete-time signal or system x[n] is given by:

[Tex]X(z)=\sum_{n= -\infty}^{ \infty}x[n].z^{-n}[/Tex]

The ROC for the Z-transform is the set of complex values z for which this sum converges absolutely. In other words, it’s the set of values of z for which the series is finite.

ROC of Laplace Transform

It is the range of Complex variable ‘s’ in s-plane for which the Laplace Transform is finite of convergent.

The Laplace transform of a continuous-time signal or system x(t) is given by:

X(s)=\int_{0}^{\infty}x(t).e^{-st}dt

The ROC for the Laplace transform is the set of complex values s for which this integral converges absolutely. In other words, it’s the set of values of s for which the integral is finite.

Types of Region of Convergence of the Z-Transform for Causal, Anti-causal and Non-causal signals

Given below are the ROC of Causal, Anti-causal and Non-causal signals

ROC for z-Transform of Causal Signals is given below

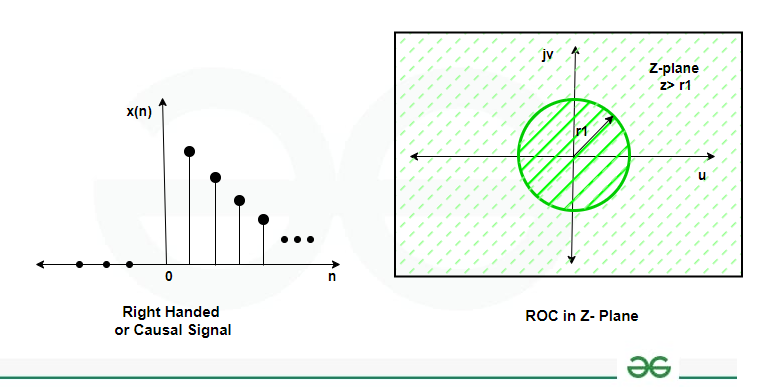
ROC for z-Transform of Causal Signals

ROC of Z- transform for an Anti-Causal signal is given below

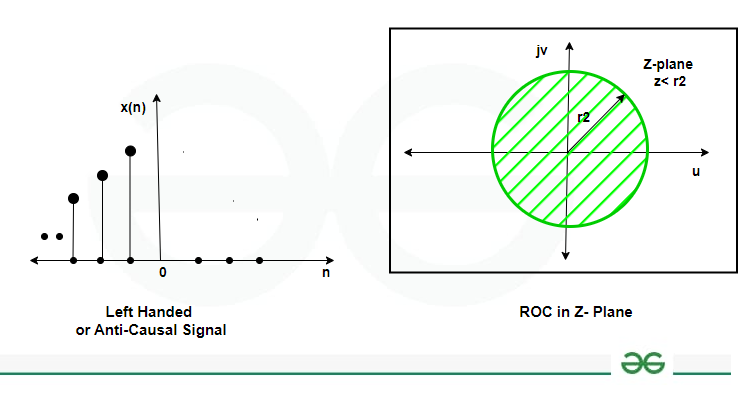
ROC of Z- transform for an Anti-Causal signal

ROC of Z-Transform for a Non-Causal Signal is given below

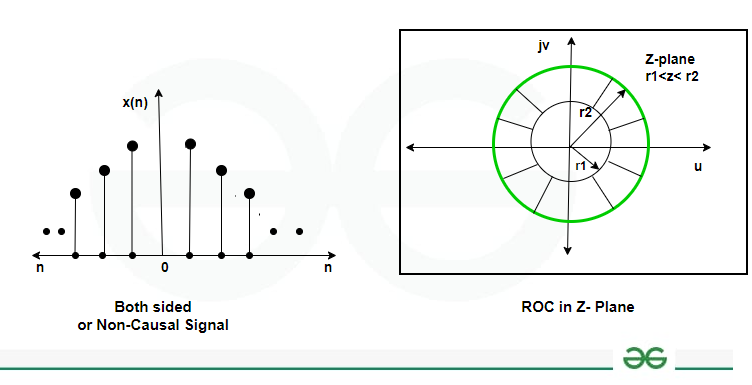
ROC of Z-Transform for a Non-Causal Signal

Properties of Region of Convergence of Z- Transform

• ROC of a signal X(z) consists of a ring in the z-plane which is centered about the origin.
• If the Z-Transform of a signal i.e. X(z) is rational, then ROC does not contains any Poles.
• If x(n) is of finite duration and absolutely summable ( for n= -∞ to +∞) then, ROC is the entire z-plane, except for z=0 or z=∞.
• If x(n) is right-sided and of infinite duration (i.e., x(n) = 0 for all n< N1 ; for finite N1 ), then the ROC is the region in the a plane outside the outermost pole i.e., outside the circle of radius equal to the largest magnitude of the pole of X(z). Furthermore, if x(n) is causal (i.e., if it is right-sided and equal to 0 for n< then the ROC also includes z=∞.
• If x(n) is left-sided and of infinite duration (i.e., x(n) = 0 for all | n > N2 ; for finite N2 ), then the ROC is the region in the z-plane inside the innermost pole i.e., inside the circle of radius equal to the smallest magnitude of the poles of X(z) other than any at z=0 and extending inward to and possibly including z = 0. In particular, if x(n) is anti-causal (i.e., if it is left-sided and equal to 0 for n>0 ), then the ROC also includes z=0.
• If x(n) is two-sided and of infinite duration (i.e., the signal is of infinite extent for both n < 0 and n > 0), then the ROC will consist of a ring in the z-plane.
• For a finite-duration right-sided signal (i.e., x(n) = 0 for n < 0 and n > N1 for some finite N1 ), the ROC will be the entire -plane except z=0.
• For a finite-duration two-sided signal (i.e., the signal is of finite extent for both n<0 and n>0), the ROC will be the entire z-plane except z=0 and z= ∞.
• For a finite-duration left-sided signal (i.e., x(n)=0 for n > 0 and n <-N1 for some finite positive N1), the ROC will be the entire z-plane except z=∞.

Advantages of ROC of Z-Transform

• The ROC provides information about a system’s stability, causality, and design parameters, ensuring mathematical well-behavior.
• It also helps in understanding the frequency response of discrete-time systems, guiding decision-making in filtering and spectral analysis.
• The ROC is a crucial tool for analyzing the stability of a system, as it includes the unit circle in the Z-plane.
• The ROC is crucial for designing digital filters, as its shape and extent influence parameters like filter order and filter type, and can guide design decisions effectively.
• ROC analysis discrete-time systems’ frequency response, analyzing the poles and zeros, crucial for signal processing applications like filtering and spectral analysis.

Disadvantages of ROC of Z-Transform

• The ROC provides limited information on the Z-transform’s convergence behavior, only indicating its convergence in the complex plane, without specifying convergence within the ROC itself.
• Interpreting the ROC, for sequences with complex or non-standard behavior, can be difficult due to its complexity.
• The ROC is not unique for a sequence, and different choices can lead to different interpretations of system properties, making it hard to find a unique solution.
• It assumes causality, making it unsuitable for non-causal systems or sequences.
• It requires complex calculations or impossible in some cases make ROC determination challenging in practical applications.

Applications of ROC of Z-Transform

• ROC provides information on the stability of discrete-time systems. A system is stable if its impulse response is absolutely summable, directly related to the ROC of its Z-transform.
• Understanding the ROC aids in designing digital filters, influencing design parameters and performance characteristics.
• ROC aids in analyzing and processing signals in digital signal processing (DSP), facilitating operations like filtering, modulation, and spectral analysis.
• ROC plays a role in determining system stability and transient response in controllers and compensators.
• ROC aids in modeling system components, ensuring proper signal processing and transmission in communication channels.

Conclusion

In summary, the Z-transform is a crucial tool in the analysis and design of discrete-time systems and signals. A key notion in this process is the Region of Convergence (ROC). It functions as a crucial indicator of communication system performance, control system behavior, signal processing activities, filter design viability, and system stability.

Engineers may ensure the dependability, effectiveness, and efficiency of digital systems and processes by making sound decisions across a range of domains by comprehending the ROC. As a result, the ROC is a fundamental component of both the theoretical and practical applications of system analysis and discrete-time signal processing.

Properties of Region of Convergence (ROC) of the Z-Transform – FAQs

Can various signals or systems have an impact on the ROC?

Various systems or signals may exhibit different ROCs, which are indication of their distinct causality and stability characteristics. The z-Transform function, on the other hand, is constant even though the ROC might vary since the z-Transform itself is specific to a particular signal or system.

How is ROC represented in a z-plane?

In the z-plane, the ROC is often shown as a shaded region. Unbounded regions can be represented by dashed lines that reach infinity, whereas bounded part are typically darkened. Other important locations, such as poles and zeros, are indicated in the z-plane to help understand how they affect the ROC.

What occurs if the ROC is either undefined or not specified?

The convergence characteristics of the z-Transform cannot be determined if the ROC is either undefined or not provided. This uncertainty may cause the signal or system to be analyzed incorrectly, which could lead to incorrect conclusions about stability, causality, and other important characteristics.