Proof that traveling salesman problem is NP Hard
Last Updated :
04 Jun, 2020
Pre-requisite: Travelling Salesman Problem,
NP Hard
Given a set of cities and the distance between each pair of cities, the
travelling salesman problem finds the path between these cities such that it is the shortest path and traverses every city once, returning back to the starting point.
Problem – Given a graph
G(V, E), the problem is to determine if the graph has a TSP consisting of cost at most
K.
Explanation –
In order to prove the Travelling Salesman Problem is NP-Hard, we will have to reduce a known NP-Hard problem to this problem. We will carry out a reduction from the Hamiltonian Cycle problem to the Travelling Salesman problem.
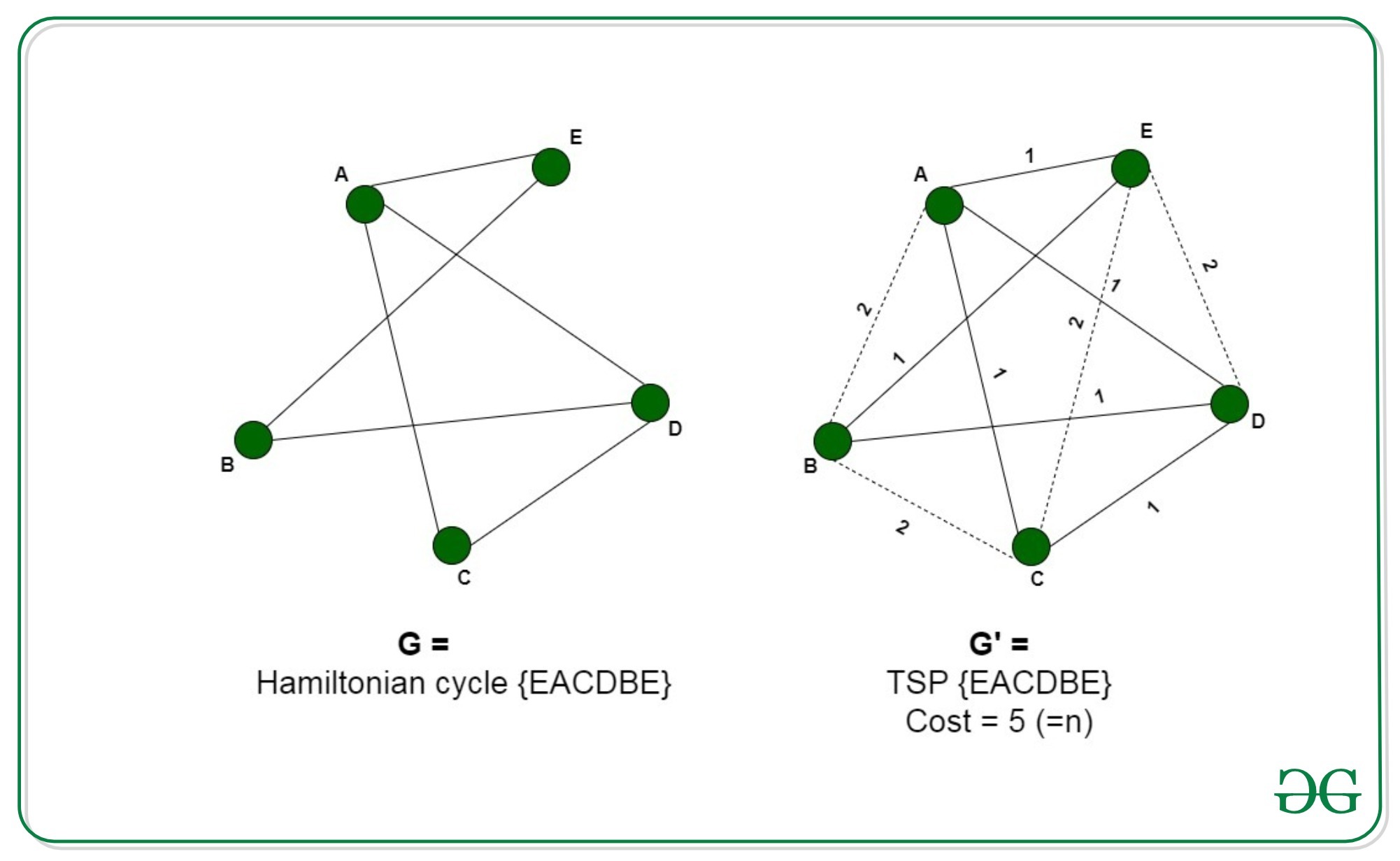
Every instance of the Hamiltonian Cycle problem consists of a graph G =(V, E) as the input can be converted to a Travelling Salesman problem consisting of graph G’ = (V’, E’) and the maximum cost, K. We will construct the graph G’ in the following way:
For all the edges e belonging to E, add the cost of edge c(e)=1. Connect the remaining edges, e’ belonging to E’, that are not present in the original graph
G, each with a cost c(e’)= 2.
And, set
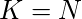
.
The new graph G’ can be constructed in polynomial time by just converting G to a complete graph G’ and adding corresponding costs. This reduction can be proved by the following two claims:
- Let us assume that the graph G contains a Hamiltonian Cycle, traversing all the vertices V of the graph. Now, these vertices form a TSP with
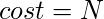 Since it uses all the edges of the original graph having cost c(e)=1. And, since it is a cycle, therefore, it returns back to the original vertex.
Since it uses all the edges of the original graph having cost c(e)=1. And, since it is a cycle, therefore, it returns back to the original vertex.
- We assume that the graph G’ contains a TSP with cost,
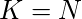 . The TSP traverses all the vertices of the graph returning to the original vertex. Now since none of the vertices are excluded from the graph and the cost sums to n, therefore, necessarily it uses all the edges of the graph present in E, with cost 1, hence forming a hamiltonian cycle with the graph G.
. The TSP traverses all the vertices of the graph returning to the original vertex. Now since none of the vertices are excluded from the graph and the cost sums to n, therefore, necessarily it uses all the edges of the graph present in E, with cost 1, hence forming a hamiltonian cycle with the graph G.
Thus we can say that the graph
G’ contains a TSP if graph
G contains Hamiltonian Cycle. Therefore, any instance of the Travelling salesman problem can be reduced to an instance of the hamiltonian cycle problem. Thus, the TSP is NP-Hard.
Share your thoughts in the comments
Please Login to comment...