Program to implement Linear Extrapolation
Last Updated :
17 Apr, 2023
What is Extrapolation?
Extrapolation is the process in mathematics where the required value is estimated beyond the range of the given variable range. Extrapolation is often used to estimate the data of some observation below or above the given range. Extrapolation is also referred to as a mathematical prediction to predict values by observing the relationship between the given variables. There are many processes of Extrapolation.Here only Linear Extrapolation will be discussed. This process was first described by Thomas D. Clareson in 1959 in his book of science. He referred to it as a meaningful prediction by understanding the given data.
How to calculate Linear Exptrapolation?
The method is useful when the linear function is given. It is done by drawing a tangent and extending it beyond the limit. Linear Extrapolation gives a very good result when the point to be predicted is not very far from the rest of the points.
Extrapolation formula: 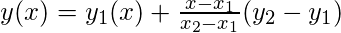
Here 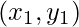 and
and 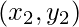 are two given points and x is the point for which we want to predict the value of y.
are two given points and x is the point for which we want to predict the value of y.
Examples:
Input: 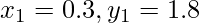 ,
, 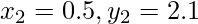 , x = 1.2
, x = 1.2
Output: y = 3.15

Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
struct Data {
double x, y;
};
double extrapolate(Data d[], double x)
{
double y;
y = d[0].y
+ (x - d[0].x)
/ (d[1].x - d[0].x)
* (d[1].y - d[0].y);
return y;
}
int main()
{
Data d[] = { { 1.2, 2.7 }, { 1.4, 3.1 } };
double x = 2.1;
cout << "Value of y at x = 2.1 : "
<< extrapolate(d, x);
return 0;
}
|
Java
class GFG
{
static double extrapolate(double[][] d, double x)
{
double y = d[0][1] + (x - d[0][0]) /
(d[1][0] - d[0][0]) *
(d[1][1] - d[0][1]);
return y;
}
public static void main (String[] args)
{
double[][] d = {{ 1.2, 2.7 },{ 1.4, 3.1 }};
double x = 2.1;
System.out.println("Value of y at x = 2.1 : " +
extrapolate(d, x));
}
}
|
Python3
def extrapolate(d, x):
y = (d[0][1] + (x - d[0][0]) /
(d[1][0] - d[0][0]) *
(d[1][1] - d[0][1]));
return y;
d = [[ 1.2, 2.7 ], [1.4, 3.1 ]];
x = 2.1;
print("Value of y at x = 2.1 :",
extrapolate(d, x));
|
C#
class GFG
{
static double extrapolate(double[,] d, double x)
{
double y = d[0,1] + (x - d[0,0]) /
(d[1,0] - d[0,0]) *
(d[1,1] - d[0,1]);
return y;
}
static void Main()
{
double[,] d = {{ 1.2, 2.7 },{ 1.4, 3.1 }};
double x = 2.1;
System.Console.WriteLine("Value of y at x = 2.1 : " +
extrapolate(d, x));
}
}
|
PHP
<?php
function extrapolate($d, $x)
{
$y = $d[0][1] + ($x - $d[0][0]) /
($d[1][0] - $d[0][0]) *
($d[1][1] - $d[0][1]);
return $y;
}
$d = array(array( 1.2, 2.7 ),
array( 1.4, 3.1 ));
$x = 2.1;
echo "Value of y at x = 2.1 : ",
extrapolate($d, $x);
?>
|
Javascript
<script>
function extrapolate(d, x)
{
let y = d[0][1] + (x - d[0][0]) / (d[1][0] - d[0][0]) *
(d[1][1] - d[0][1]);
return y;
}
let d = [[ 1.2, 2.7 ],[ 1.4, 3.1 ]];
let x = 2.1;
document.write("Value of y at x = 2.1 : " +
extrapolate(d, x));
</script>
|
Output: Value of y at x = 2.1 : 4.5
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...