Program to implement Simpson’s 3/8 rule
Last Updated :
21 Sep, 2022
Write a program to implement Simpson’s 3/8 rule.
The Simpson’s 3/8 rule was developed by Thomas Simpson. This method is used for performing numerical integrations. This method is generally used for numerical approximation of definite integrals. Here, parabolas are used to approximate each part of curve.
Simpson’s 3/8 formula :
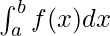 =
= 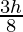 [Tex]( [/Tex]F(a) + 3F
[Tex]( [/Tex]F(a) + 3F 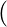 [Tex]\frac{2a + b}{3} ) [/Tex]+ 3F
[Tex]\frac{2a + b}{3} ) [/Tex]+ 3F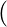 [Tex]\frac{a + 2b}{3} ) [/Tex]+ F(b)
[Tex]\frac{a + 2b}{3} ) [/Tex]+ F(b) 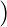
Here,
h is the interval size given by h = ( b – a ) / n
n is number of intervals or interval limit
Examples :
Input : lower_limit = 1, upper_limit = 10,
interval_limit = 10
Output : integration_result = 0.687927
Input : lower_limit = 1, upper_limit = 5,
interval_limit = 3
Output : integration_result = 0.605835
C++
#include<iostream>
using namespace std;
float func( float x)
{
return (1 / ( 1 + x * x ));
}
float calculate(float lower_limit, float upper_limit,
int interval_limit )
{
float value;
float interval_size = (upper_limit - lower_limit)
/ interval_limit;
float sum = func(lower_limit) + func(upper_limit);
for (int i = 1 ; i < interval_limit ; i++)
{
if (i % 3 == 0)
sum = sum + 2 * func(lower_limit + i * interval_size);
else
sum = sum + 3 * func(lower_limit + i * interval_size);
}
return ( 3 * interval_size / 8 ) * sum ;
}
int main()
{
int interval_limit = 10;
float lower_limit = 1;
float upper_limit = 10;
float integral_res = calculate(lower_limit, upper_limit,
interval_limit);
cout << integral_res;
return 0;
}
|
Java
import java.util.*;
class GFG {
static float func( float x)
{
return (1 / ( 1 + x * x ));
}
static float calculate(float lower_limit,
float upper_limit, int interval_limit )
{
float value;
float interval_size = (upper_limit - lower_limit)
/ interval_limit;
float sum = func(lower_limit) + func(upper_limit);
for (int i = 1 ; i < interval_limit ; i++)
{
if (i % 3 == 0)
sum = sum + 2 * func(lower_limit
+ i * interval_size);
else
sum = sum + 3 * func(lower_limit + i
* interval_size);
}
return ( 3 * interval_size / 8 ) * sum ;
}
public static void main(String[] args)
{
int interval_limit = 10;
float lower_limit = 1;
float upper_limit = 10;
float integral_res = calculate(lower_limit, upper_limit,
interval_limit);
System.out.println(integral_res);
}
}
|
Python3
def func(x):
return (float(1) / ( 1 + x * x ))
def calculate(lower_limit, upper_limit, interval_limit ):
interval_size = (float(upper_limit - lower_limit) / interval_limit)
sum = func(lower_limit) + func(upper_limit);
for i in range(1, interval_limit ):
if (i % 3 == 0):
sum = sum + 2 * func(lower_limit + i * interval_size)
else:
sum = sum + 3 * func(lower_limit + i * interval_size)
return ((float( 3 * interval_size) / 8 ) * sum )
interval_limit = 10
lower_limit = 1
upper_limit = 10
integral_res = calculate(lower_limit, upper_limit, interval_limit)
print (round(integral_res, 6))
|
C#
using System;
class GFG {
static float func( float x)
{
return (1 / ( 1 + x * x ));
}
static float calculate(float lower_limit,
float upper_limit, int interval_limit )
{
float interval_size = (upper_limit - lower_limit)
/ interval_limit;
float sum = func(lower_limit) + func(upper_limit);
for (int i = 1 ; i < interval_limit ; i++)
{
if (i % 3 == 0)
sum = sum + 2 * func(lower_limit
+ i * interval_size);
else
sum = sum + 3 * func(lower_limit + i
* interval_size);
}
return ( 3 * interval_size / 8 ) * sum ;
}
public static void Main()
{
int interval_limit = 10;
float lower_limit = 1;
float upper_limit = 10;
float integral_res = calculate(lower_limit, upper_limit,
interval_limit);
Console.WriteLine(integral_res);
}
}
|
PHP
<?php
function func( $x)
{
return (1 / ( 1 + $x * $x ));
}
function calculate($lower_limit, $upper_limit,
$interval_limit)
{
$interval_size = ($upper_limit -
$lower_limit) /
$interval_limit;
$sum = func($lower_limit) +
func($upper_limit);
for ($i = 1 ; $i < $interval_limit ; $i++)
{
if ($i % 3 == 0)
$sum = $sum + 2 * func($lower_limit +
$i * $interval_size);
else
$sum = $sum + 3 * func($lower_limit +
$i * $interval_size);
}
return ( 3 * $interval_size / 8 ) * $sum ;
}
$interval_limit = 10;
$lower_limit = 1;
$upper_limit = 10;
$integral_res = calculate($lower_limit, $upper_limit,
$interval_limit);
echo $integral_res;
?>
|
Javascript
<script>
function func(x)
{
return (1 / ( 1 + x * x ));
}
function calculate(lower_limit,
upper_limit, interval_limit )
{
let value;
let interval_size = (upper_limit - lower_limit)
/ interval_limit;
let sum = func(lower_limit) + func(upper_limit);
for (let i = 1 ; i < interval_limit ; i++)
{
if (i % 3 == 0)
sum = sum + 2 * func(lower_limit
+ i * interval_size);
else
sum = sum + 3 * func(lower_limit + i
* interval_size);
}
return ( 3 * interval_size / 8 ) * sum ;
}
let interval_limit = 10;
let lower_limit = 1;
let upper_limit = 10;
let integral_res = calculate(lower_limit, upper_limit,
interval_limit);
document.write(integral_res);
</script>
|
Output :
0.687927
Time Complexity: O(interval_limit)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...