Program to find the Nth term of the series 3, 7, 13, 21, 31…..

Given a number N, the task is to find the Nth term of this series:

3, 7, 13, 21, 31, …….

Examples:

Input: N = 4
Output: 21
Explanation:
Nth term = (pow(N, 2) + N + 1)
         = (pow(4, 2) + 4 + 1)
         = 21

Input: N = 11
Output: 133

Approach:

Subtracting these two equations we get 

Therefore, the Nth Term of the given series is: 

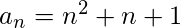
Below is the implementation of the above approach: 

C++

// CPP program to find the Nth term of given series.
#include <iostream>
#include <math.h>
using namespace std;

// Function to calculate sum
long long int getNthTerm(long long int N)
{
    // Return Nth term
    return (pow(N, 2) + N + 1);
}

// driver code
int main()
{
    // declaration of number of terms
    long long int N = 11;

    // Get the Nth term
    cout << getNthTerm(N);

    return 0;
}

Java

// Java code to find the Nth term of given series.
import java.util.*;

class solution
{

// Function to calculate sum
static long getNthTerm(long N)
{

   // Return Nth term
    return ((int)Math.pow(N, 2) + N + 1);
}

//Driver program
public static void main(String arr[])
{

   // declaration of number of terms
    long N = 11;

    // Get the Nth term
    System.out.println(getNthTerm(N));

}
}
//THis code is contributed by
//Surendra_Gangwar

Python3

# Python3 Code to find the
# Nth term of given series.

# Function to calculate sum
def getNthTerm(N):

    # Return Nth term
    return (pow(N, 2) + N + 1)

# driver code
if __name__=='__main__':

# declaration of number of terms
    N = 11

# Get the Nth term
    print(getNthTerm(N))

# This code is contributed by
# Sanjit_Prasad

C#

// C# code to find the Nth
// term of given series.
using System;

class GFG
{

// Function to calculate sum
static long getNthTerm(long N)
{

// Return Nth term
    return ((int)Math.Pow(N, 2) + N + 1);
}

// Driver Code
static public void Main ()
{

    // declaration of number
    // of terms
    long N = 11;

    // Get the Nth term
    Console.Write(getNthTerm(N));
}
}

// This code is contributed by Raj

PHP

<?php
// PHP program to find the
// Nth term of given series

// Function to calculate sum
function getNthTerm($N)
{
    // Return Nth term
    return (pow($N, 2) + $N + 1);
}

// Driver code

// declaration of number of terms
$N = 11;

// Get the Nth term
echo getNthTerm($N);

// This code is contributed by Raj
?>

Javascript

<script>
// JavaScript program to find the Nth term of given series.

// Function to calculate sum
function getNthTerm(N)
{
    // Return Nth term
    return (Math.pow(N, 2) + N + 1);
}

// driver code

   // declaration of number of terms
   let N = 11;

   // Get the Nth term
   document.write(getNthTerm(N));

// This code is contributed by Surbhi Tyagi

</script>

Output:

133

Time Complexity: O(1)
Space Complexity: O(1) since using constant variables

Method 2: We can also solve the problem by the formula [ (n+1)²-n  ]. 

C++

// CPP program to find the Nth term of given series.
#include <iostream>
#include <math.h>
using namespace std;

// Function to calculate sum
long long int getNthTerm(long long int N)
{
    // Return Nth term
    return (pow(N + 1, 2) - N);
}

// driver code
int main()
{
    // declaration of number of terms
    long long int N = 11;

    // Get the Nth term
    cout << getNthTerm(N);

    return 0;
}

Python3

# Python program to find the Nth term of given series.
import math

# Function to calculate sum
def getNthTerm(N):
    # Return Nth term
    return int(math.pow(N + 1, 2) - N)

# driver code
if __name__ == '__main__':
    # declaration of number of terms
    N = 11

    # Get the Nth term
    print(getNthTerm(N))

Output

133

Time Complexity: O(logN)
Space Complexity: O(1) since using constant variables