Program to find sum of first n natural numbers

Given a number n, find the sum of the first natural numbers.

Examples :

Input: n = 3
Output: 6
Explanation:
Note that 1 + 2 + 3 = 6

Input  : 5
Output : 15 
Explanation :
Note that 1 + 2 + 3 + 4 + 5 = 15

Program to Find the Sum of First N Natural Numbers

A simple solution is to do the following.

1) Initialize : sum = 0
2) Run a loop from x = 1 to n and 
   do following in loop.
     sum = sum + x

C

// C program to find sum of first
// n natural numbers.
#include <stdio.h>
 
// Returns sum of first n natural
// numbers
int findSum(int n)
{
    int sum = 0;
    for (int x = 1; x <= n; x++)
        sum = sum + x;
    return sum;
}
 
// Driver code
int main()
{
    int n = 5;
    printf("%d", findSum(n));
    return 0;
}

C++

// CPP program to find sum of first
// n natural numbers.
#include <iostream>
using namespace std;
 
// Returns sum of first n natural
// numbers
int findSum(int n)
{
    int sum = 0;
    for (int x = 1; x <= n; x++)
        sum = sum + x;
    return sum;
}
 
// Driver code
int main()
{
    int n = 5;
    cout << findSum(n);
    return 0;
}

Java

// JAVA program to find sum of first
// n natural numbers.
import java.io.*;
 
class GFG{
 
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        int sum = 0;
        for (int x = 1; x <= n; x++)
            sum = sum + x;
        return sum;
    }
 
    // Driver code
    public static void main(String args[])
    {
        int n = 5;
        System.out.println(findSum(n));
    }
}
 
// This code is contributed by Nikita Tiwari.

Python3

# PYTHON program to find sum of first
# n natural numbers.
 
# Returns sum of first n natural
# numbers
def findSum(n):
    sum = 0
    x = 1
    while x <= n:
        sum = sum + x
        x = x + 1
    return sum
 
 
# Driver code
n = 5
print findSum(n)

C#

// C# program to find sum of first
// n natural numbers.
using System;
 
class GFG{
 
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        int sum = 0;
        for (int x = 1; x <= n; x++)
            sum = sum + x;
        return sum;
    }
 
    // Driver code
    public static void Main()
    {
        int n = 5;
        Console.Write(findSum(n));
    }
}
 
// This code is contributed by vt_m.

PHP

<?php
// PHP program to find sum of first
// n natural numbers.
 
// Returns sum of first n natural
// numbers
function findSum($n)
{
$sum = 0;
for ($x = 1; $x <= $n; $x++)
    $sum = $sum + $x;
return $sum;
}
 
// Driver code
$n = 5;
echo findSum($n);
 
// This code is contributed by Sam007
?>

Javascript

<script>
// Javascript program to find sum of first
// n natural numbers.
 
// Returns sum of first n natural
// numbers
function findSum(n)
{
   let sum = 0;
   for (let x = 1; x <= n; x++)
     sum = sum + x;
   return sum;
}
 
// Driver code
let n = 5;
document.write(findSum(n));
 
// This code is contributed by rishavmahato348.
</script>

Output

Time Complexity: O(n)

Auxiliary Space: O(1)

Optimized solution to find Sum of n Natural Numbers in Python

An efficient solution is to use the below formula.

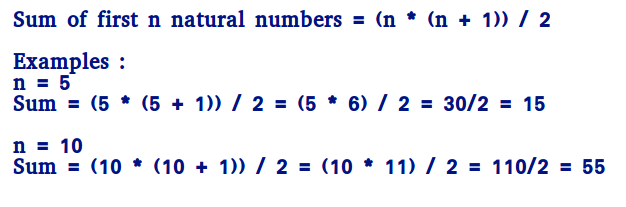
How does this work?

We can prove this formula using induction.

It is true for n = 1 and n = 2
For n = 1, sum = 1 * (1 + 1)/2 = 1
For n = 2, sum = 2 * (2 + 1)/2 = 3

Let it be true for k = n-1.

Sum of k numbers = (k * (k+1))/2
Putting k = n-1, we get
Sum of k numbers = ((n-1) * (n-1+1))/2
                 = (n - 1) * n / 2

If we add n, we get,
Sum of n numbers = n + (n - 1) * n / 2
                 = (2n + n² - n)/2
                 = n * (n + 1)/2

C

// Efficient C program to find
// sum of first n natural numbers.
#include<stdio.h>
 
// Returns sum of first n natural
// numbers
int findSum(int n)
{
   return n * (n + 1) / 2;
}
 
// Driver code
int main()
{
  int n = 5;
  printf("%d", findSum(n));
  return 0;
}

C++

// Efficient CPP program to find sum of first
// n natural numbers.
#include<iostream>
using namespace std;
 
// Returns sum of first n natural
// numbers
int findSum(int n)
{
   return n * (n + 1) / 2;
}
 
// Driver code
int main()
{
  int n = 5;
  cout << findSum(n);
  return 0;
}

Java

// Efficient JAVA program to find sum
// of first n natural numbers.
import java.io.*;
 
class GFG{
     
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        return n * (n + 1) / 2;
    }
 
    // Driver code
    public static void main(String args[])
    {
        int n = 5;
        System.out.println(findSum(n));
    }
}
 
// This code is contributed by Nikita Tiwari.

Python3

# Efficient CPP program to find sum
# of first n natural numbers.
 
# Returns sum of first n natural
# numbers
def findSum(n) :
    return n * (n + 1) / 2
     
# Driver code
n = 5
print findSum(n)
 
# This code is contributed by Nikita Tiwari.

C#

// Efficient C# program to find sum
// of first n natural numbers.
using System;
 
class GFG{
     
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        return n * (n + 1) / 2;
    }
 
    // Driver code
    public static void Main()
    {
        int n = 5;
        Console.Write(findSum(n));
    }
}
 
// This code is contributed by vt_m.

php

<?php
// Efficient PHP program to find sum
// of first n natural numbers.
 
// Returns sum of first n natural
// numbers
function findSum($n)
{
    return ($n * ($n + 1) / 2);
}
 
// Driver code
$n = 5;
echo findSum($n);
 
// This code is contributed by Sam007
?>

Javascript

<script>
// javascript Program to find the average
// of sum of first n natural numbers
 
// Return the average of sum
// of first n even numbers
function findSum(n)
{
    return n * (n + 1) / 2;
}
var n = 5;
document.write(findSum(n));
 
// This code is contributed by sravan kumar
</script>

Output

Time Complexity: O(1)

Auxiliary Space: O(1)

The above program causes overflow, even if the result is not beyond the integer limit. We can avoid overflow up to some extent by dividing first.

C

// Efficient C program to find
// sum of first n natural numbers
// that avoids overflow if result
// is going to be within limits.
#include<stdio.h>
  
// Returns sum of first n natural
// numbers
int findSum(int n)
{
   if (n % 2 == 0)
      
      // Here multiplying by 1LL help to
      // perform calculations in long long,
      // so that answer should not be overflowed
      return (n / 2) * 1LL * (n + 1);
  
   // If n is odd, (n+1) must be even
   else
      
      // Here multiplying by 1LL help to
      // perform calculations in long long,
      // so that answer should not be overflowed
      return  ((n + 1) / 2) * 1LL * n;
}
  
// Driver code
int main()
{
  int n = 5;
  printf("%d", findSum(n));
  return 0;
}

C++

// Efficient CPP program to find sum of first
// n natural numbers that avoids overflow if
// result is going to be within limits.
#include<iostream>
using namespace std;
  
// Returns sum of first n natural
// numbers
int findSum(int n)
{
   if (n % 2 == 0)
       
      // Here multiplying by 1LL help to
      // perform calculations in long long,
      // so that answer should not be overflowed
      return (n / 2) * 1LL * (n + 1);
  
   // If n is odd, (n+1) must be even
   else
      
      // Here multiplying by 1LL help to
      // perform calculations in long long,
      // so that answer should not be overflowed
      return  ((n + 1) / 2) * 1LL * n;
}
  
// Driver code
int main()
{
  int n = 5;
  cout << findSum(n);
  return 0;
}

Java

// Efficient JAVA program to find sum of first
// n natural numbers that avoids overflow if
// result is going to be within limits.
import java.io.*;
 
class GFG{
 
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        if (n % 2 == 0)
            return (n / 2) * (n + 1);
 
        // If n is odd, (n+1) must be even
        else
            return ((n + 1) / 2) * n;
    }
 
    // Driver code
    public static void main(String args[])
    {
        int n = 5;
        System.out.println(findSum(n));
    }
}
 
//This code is contributed by Nikita Tiwari.

Python3

# Efficient Python program to find the sum
# of first n natural numbers that avoid
# overflow if the result is going to be
# within limits.
 
# Returns sum of first n natural
# numbers
def findSum(n):
    if (n % 2 == 0):
        return (n / 2) * (n + 1)
 
   # If n is odd, (n+1) must be even
    else:
        return ((n + 1) / 2) * n
 
 
# Driver code
n = 5
print findSum(n)
 
# This code is contributed by Nikita Tiwari.

C#

// Efficient C# program to find the sum of first
// n natural numbers that avoid overflow if
// result is going to be within limits.
using System;
 
class GFG{
 
    // Returns sum of first n natural
    // numbers
    static int findSum(int n)
    {
        if (n % 2 == 0)
            return (n / 2) * (n + 1);
 
        // If n is odd, (n+1) must be even
        else
            return ((n + 1) / 2) * n;
    }
 
    // Driver code
    public static void Main()
    {
        int n = 5;
        Console.Write(findSum(n));
    }
}
 
// This code is contributed by vt_m.

PHP

<?php
// Efficient php program to find sum of first
// n natural numbers that avoids overflow if
// result is going to be within limits.
 
// Returns sum of first n natural
// numbers
function findSum($n)
{
    if ($n % 2 == 0)
        return ($n / 2) *
               ($n + 1);
     
    // If n is odd, (n+1) must be even
    else
        return (($n + 1) / 2) * $n;
}
 
// Driver code
$n = 5;
echo findSum($n);
 
// This code is contributed by Sam007
?>

Javascript

<script>
//efficient approach using  javascript to find the average
// of sum of first n natural numbers
 
// Return the average of sum
// of first n even numbers
function findSum(n)
{
    if (n % 2 == 0)
        return (n / 2) * (n + 1)
 
// If n is odd, (n+1) must be even
    else
    return ((n + 1) / 2) * n
         
}
var n = 5;
document.write(findSum(n));
 
// This code is contributed by sravan kumar
</script>