Find the Nth term of the series 3, 5, 9, 17, 33. . .
Last Updated :
16 Aug, 2022
Given a positive integer N, the task is to find Nth term of the series-
3, 5, 9, 17, 33…till N terms
Examples:
Input: N = 4
Output: 17
Input: N = 3
Output: 9
Approach:
Consider the below example:
Lets say N = 4
The 4th term of the given series is 17, i.e. : 2 ^ 4 + 1 = 16 + 1 = 17
Similarly, lets say N = 3
The 3rd term of the given series is : 2 ^ 3 + 1 = 8 + 1 = 9 (which is correct).
Therefore, we can find out the relation for Nth term of the series using above observations:
1st term = 3 = 21 + 1
2nd term = 22 + 1 = 5
3rd term = 23 + 1 = 9
4th term = 24 + 1 = 17
.
.
Therefore, Nth term can be found out using following relation: 2N + 1
Upon generalising, the relation for Nth term can be represented as:
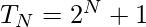
Below is the implementation of the above approach-
C++
#include <bits/stdc++.h>
using namespace std;
int findTerm(int N)
{
return pow(2, N) + 1;
}
int main()
{
int N = 6;
cout << findTerm(N);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int findTerm(int N)
{
return (int)Math.pow(2, N) + 1;
}
public static void main (String[] args)
{
int N = 6;
System.out.print(findTerm(N));
}
}
|
Python3
def findTerm(N):
return (2 ** N) + 1;
N = 6;
print(findTerm(N));
|
C#
using System;
class GFG
{
static int findTerm(int N)
{
return (int)Math.Pow(2, N) + 1;
}
public static void Main()
{
int N = 6;
Console.Write(findTerm(N));
}
}
|
Javascript
<script>
const findTerm = (N) => {
return Math.pow(2, N) + 1;
}
let N = 6;
document.write(findTerm(N));
</script>
|
Time Complexity: O(logN) because it using inbuilt pow function
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...