Program to evaluate the expression (√X+1)^6 + (√X-1)^6
Last Updated :
19 Jul, 2022
Given a number 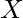 . The task is to find the value of the below expression for the given value of
. The task is to find the value of the below expression for the given value of 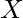 .
.
![Rendered by QuickLaTeX.com (\sqrt[]{X} +1)^6 + (\sqrt[]{X}-1)^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-000155483878454669c3868ddf11c6e8_l3.png)
Examples:
Input: X = ?2
Output: 198
Explanation: ![Rendered by QuickLaTeX.com 2[(\sqrt[]{2})^6 + 15 (\sqrt[]{2})^4 + 15\sqrt[]{2})^2 + 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f9773864c854d0406eeae560978fd32_l3.png)
= 198
Input: X = 3
Output: 4160
Approach: The idea is to use Binomial expression. We can take these two terms as 2 binomial expressions. By expanding these terms we can find the desired sum. Below is the expansion of the terms.
![Rendered by QuickLaTeX.com \newline (X+1)^6 = {6_C}_0 X^6+6_c_1 X^5+{6_C}_2 X^4+{6_C}_3 X^3+{6_C}_4 X^2+{6_C}_5 X+{6_C}_6 \newline (X-1)^6 = {6_C}_0 X^6-6_c_1 X^5+{6_C}_2 X^4-{6_C}_3 X^3+{6_C}_4 X^2-{6_C}_5 X+{6_C}_6 \newline (X+1)^6+(X-1)^6 =2[{6_C}_0 X^6+{6_C}_2 X^4+{6_C}_4 X^2+{6_C}_6] \newline \newline (X+1)^6+(X-1)^6=2[X^6 + 15 X^4 + 15 X^2 +1] ---EQ(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-901fbe3374ba17dadf2bebb174fee90b_l3.png)
Now put X=  in EQ(1)
in EQ(1)
![Rendered by QuickLaTeX.com \newline (\sqrt[]{2}+1)^6+(\sqrt[]{2}-1)^6 = 2[(\sqrt[]{2})^6 + 15 (\sqrt[]{2})^4 + 15\sqrt[]{2})^2 + 1] \newline = 2(8 + 15 x 4 + 15 x 2 + 1 ) \newline = 2(8 + 60 + 30 + 1) \newline = 198](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddf6a609f8f3e1b8fd7019f95eae37cf_l3.png)
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float calculateSum(float n)
{
int a = int(n);
return 2 * (pow(n, 6) + 15 * pow(n, 4)
+ 15 * pow(n, 2) + 1);
}
int main()
{
float n = 1.4142;
cout << ceil(calculateSum(n)) << endl;
return 0;
}
|
Java
import java.util.*;
class gfg
{
public static double calculateSum(double n)
{
return 2 * (Math.pow(n, 6) + 15 * Math.pow(n, 4)
+ 15 * Math.pow(n, 2) + 1);
}
public static void main(String[] args)
{
double n = 1.4142;
System.out.println((int)Math.ceil(calculateSum(n)));
}
}
|
Python3
import math
def calculateSum(n):
a = int(n)
return (2 * (pow(n, 6) + 15 * pow(n, 4)
+ 15 * pow(n, 2) + 1))
if __name__=='__main__':
n = 1.4142
print(math.ceil(calculateSum(n)))
|
C#
using System;
class gfg
{
public static double calculateSum(double n)
{
return 2 * (Math.Pow(n, 6) + 15 * Math.Pow(n, 4)
+ 15 * Math.Pow(n, 2) + 1);
}
public static int Main()
{
double n = 1.4142;
Console.WriteLine(Math.Ceiling(calculateSum(n)));
return 0;
}
}
|
PHP
<?php
function calculateSum($n)
{
$a = (int)$n;
return (2 * (pow($n, 6) +
15 * pow($n, 4) +
15 * pow($n, 2) + 1));
}
$n = 1.4142;
echo ceil(calculateSum($n));
?>
|
Javascript
<script>
function calculateSum(n)
{
return 2 * (Math.pow(n, 6) + 15 * Math.pow(n, 4)
+ 15 * Math.pow(n, 2) + 1);
}
var n = 1.4142;
document.write(parseInt(Math.ceil(calculateSum(n))));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...