Componendo and Dividendo Rule

Componendo and Dividendo are two very uncommon rules in algebra that help us solve various problems in algebra. Componendo and Dividendo rules are defined on the basis of direct proportion and using these rules we can reduce the number of operations and the complexity of the ratios. Componendo and Dividendo are generally used where the ratio or proportion involves fractions or rational functions to simplify the equations and make calculations easier.

Other than Componendo and Dividendo there are two more similar rules algebra i.e., Alternendo and Invertendo. This article discusses the Componendo and Dividendo Rules in good detail including Componendo Rule and Dividendo Rule as well.

What is Componendo Rule?

Componendo Rule is a mathematical principle used to simplify the relationship between two proportions. It is often employed in algebra and elementary mathematics to solve equations involving proportions or ratios.

Componendo Rule states that if you have two equal ratios (fractions), and you add 1 to each ratio, the resulting ratios will still be equal.

According to componendo rule, if

a/b = c/d then (a + b)/b = (c+d)/d

Read more about Ratio and Proportions.

Componendo Rule Proof

Consider a/b = c/d

Adding 1 to both sides, we get

a/b + 1 = c/d + 1

⇒ (a+b)/b = (c+d)/d

This proves the componendo rule.

What is Dividendo Rule?

On the other hand, the Dividendo Rule is the opposite of Componendo, as it states that for two ratios which are equal, if we subtract 1 from both sides, they still remain equal. Mathematically, it is represented as follows:

If a/b = c/d then (a – b)/b = (c – d)/d

Dividendo Rule Proof

Consider a/b = c/d

Subtracting 1 from both sides, we get

a/b – 1 = c/d – 1

⇒ (a – b)/b = (c – d)/d

This proves the dividendo rule.

Componendo and Dividendo Rule

Componendo-Dividendo Rule is a combination of componendo and dividendo rules. Componendo Dividendo rule states that if we are given two numbers in a certain ratio equal to the ratio of two other numbers, then the ratio of sum and difference of the first two numbers is equal to the ratio of sum and difference of the other two numbers.

Componendo Dividendo Rule Formula

Mathematically Componendo and Dividendo Rule Formula is given as:

If a/b = c/d then (a + b)/(a – b) = (c + d)/(c – d)

Note: It is necessary to add or subtract the numerator and denominator on the both sides of the equality sign.

Componendo and Dividendo Rule Proof

Consider four numbers a, b, c, and d such that ratio of a and b is equal to ratio of c and d.

a/b = c/d

Using invertendo rule, we get:

b/a = d/c

Applying componendo rule, we get:

(a+b)/b = (c+d)/d —- (1)

Applying dividendo rule, we get:

(a-b)/b = (c-d)/d —-(2)

Dividing equation (1) and (2), we get:

(a+b)/(a-b) = (c+d)/(c-d)

Thus, componendo-dividendo rule is proved.

Some Other Rules

Apart from Componendo, Dividendo, and Componendo & Dividendo Rule, we also have some other rules:

• Invertendo Rule
• Alternendo Rule

Let’s discuss these rules in little detail.

Invertendo Rule

Invertendo rule states that if ratio of two numbers is equal to the ratio of other two numbers then inverse of the ratio of first two numbers is equal to the inverse of ratio of other two numbers. Mathematically, if:

a/b = c/d then b/a = d/c

Read more about Additive Inverse.

Alternendo Rule

Alternendo rule states that if ratio of two numbers is equal to the ratio of other two numbers then the ratio of numerators on both sides of equality is equal to the ratio of denominators on both sides of equality. Mathematically, if:

a/b = c/d then a/c = b/d

How to Apply Componendo and Dividend Rule?

Assume that we are given any fraction a/b = c/d, then we can apply componendo dividendo rule as follows:

• Step 1: Add numerator and denominator on both sides to get (a+b) and (c+d).
• Step 2: Subtract numerator and denominator on both sides to get (a-b) and (c-d).
• Step 3: Divide the values obtained in step 1 and step 2 to get (a+b)/(a-b) = (c+d)/(c-d)

Read More,

• Algebraic Expression
• Algebraic Identities
• Algebraic Formulas

Solved Examples on Componendo and Dividend Rule

Example 1: b If 2a – 5b = 0, find the ratio of (a-b) : (a+b)?

Solution:

Given 2a – 5b = 0

2a = 5b

⇒ a/b = 5/2

Applying componendo-dividendo rule, we get:

a+b/a-b = 5+2/5-2

⇒ a+b/a-b = 7/3

⇒ a-b/a+b = 3/7

Thus (a-b):(a+b) = 3:7

Example 2: If a/b = 1/3, find the ratio of (a+b)/(a-b)?

Solution:

Given a/b = 1/3

Applying componendo-dividendo rule, we get:

a+b/a-b = 1+3/1-3

⇒ a+b/a-b = 4/(-2) = -2/1

Thus (a+b) : (a-b) = -2 : 1

Example 3: If (a+b) : (a-b) = 3 : 4, find a : b?

Solution:

Given (a+b) : (a-b) = 3 : 4

Applying componendo-dividendo rule, we get:

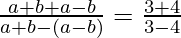
⇒ 2a/b = 7/-1

⇒ a/b = -7/2

⇒ a : b = -7 : 2

Example 4: If a = 4bc/(b+c), find the value of (a+2b)/(a-2b) + (a+2c)/(a-2c)?

Solution:

Given a = 4bc/(b+c)

⇒ a = 2b.2c/(b+c)

⇒ a/2b = 2c/(b+c)

Applying componendo-dividendo rule, we get:

a+2b/a-2b = 2c+b+c/2c-b-c

⇒ a+2b/a-2b = 3c+b/c-b . . . (1)

Now, a = 2b.2c/(b+c)

⇒ a/2c = 2b/(b+c)

Applying componendo-dividendo rule, we get:

a+2c/a-2c = 2b+b+c/2b-b-c

⇒ a+2c/a-2c = 3b+c/b-c . . . (2)

Adding(1) and (2), we get:

(a+2b)/(a-2b) + (a+2c)/(a-2c) = (3c+b/c-b) + (3b+c/b-c)

⇒ (a+2b)/(a-2b) + (a+2c)/(a-2c) = -(3c+b)/b-c + (3b+c/b-c)

⇒ (a+2b)/(a-2b) + (a+2c)/(a-2c) = -3c-b+3b+c/b-c

⇒ (a+2b)/(a-2b) + (a+2c)/(a-2c) = 2b-2c/b-c

⇒ (a+2b)/(a-2b) + (a+2c)/(a-2c) = 2

Thus, the required value of (a+2b)/(a-2b) + (a+2c)/(a-2c) is 2.

Example 5: If a/b = 5/3, find the ratio of (a-b)/(a+b)?

Solution:

Given a/b = 1/3

Applying componendo-dividendo rule, we get:

a+b/a-b = 5+3/5-3

⇒ a+b/a-b = 8/2 = 4/1

Using invertendo, we get:

a-b/a+b = 1/4

Thus (a-b) : (a+b) = 1 : 4

Componendo and Dividendo – FAQs

1. What is Componendo and Dividendo Rule?

Componenedo and Dividendo rule states that if we are given two numbers in a certain ratio equal to the ratio of two other numbers, then the ratio of sum and difference of the first two numbers is equal to the ratio of sum and difference of the other two numbers.

2. Define Invertendo Rule.

Invertendo rule states that if ratio of two numbers is equal to the ratio of other two numbers then inverse of the ratio of first two numbers is equal to the inverse of ratio of other two numbers.

3. Why do We use Componendo and Dividendo Rule?

Componendo dividendo rule is used to simplify the fractions or ratios in an equation which involve large numbers, fractions or rational numbers. It is also used to reduce the number of expansions in equation.

4. What is the Difference between Componendo Rule and Dividendo Rule?

In componendo rule, we add 1 to fraction on both sides of the equality sign whereas in dividendo rule we subtract 1 from fraction on both sides of the equality sign.

5. What is Componendo Dividendo Formula?

Componendo dividendo formula is as follows:

If a/b = c/d, then (a+b)/(a-b) = (c+d)/(c-d)

6. When is Componendo and Dividendo used?

Componendo and dividendo is a mathematical technique used to simplify and solve proportions.

7. What are the Key Properties of Componendo and Dividendo?

Componendo and dividendo, a mathematical technique for proportions, have two key properties:

• Direct Proportion: If a/b = c/d, then (a+b)/(a-b) = (c+d)/(c-d).
• Inverse Proportion: If a/b = c/d, then (a+b)/(a-b) = (d/c).

8. Are there any Limitations to using Componendo and Dividendo?

Componendo and dividendo simplifies proportions, but it only applies to certain cases, assumes non-zero denominators, and can lead to errors if misused. Its scope is limited to specific scenarios.

9. Can Componendo and Dividendo be Applied to Inequalities?

No, Componendo and Dividendo can’t be applied to inequalities, as change in sign can make the inequality infeasible.