Program to check if N is a triacontagonal number
Last Updated :
23 Nov, 2022
Given a number N, the task is to check if the number is a Triacontagonal number or not.
A Triacontagonal number is a class of figurate number. It has 30 – sided polygon called triacontagon. The N-th triacontagonal number count’s the 30 number of dots and all other dots are surrounding with a common sharing corner and make a pattern. The first few triacontagonol numbers are 1, 30, 87, 172 …
Examples:
Input: N = 30
Output: Yes
Explanation:
Second triacontagonal number is 30.
Input: 32
Output: No
Approach:
1. The Kth term of the triacontagonal number is given as:
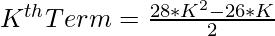
2. As we have to check whether the given number can be expressed as a triacontagonal number or not. This can be checked as follows:
=> 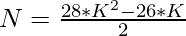
=> K = \frac{26 + \sqrt{224*N + 676}}{56}
3. Finally, check the value computed using this formula is an integer, which means that N is a triacontagonal number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool istriacontagonal(int N)
{
float n
= (26 + sqrt(224 * N + 676))
/ 56;
return (n - (int)n) == 0;
}
int main()
{
int i = 30;
if (istriacontagonal(i)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
|
Java
class GFG{
static boolean istriacontagonal(int N)
{
float n = (float) ((26 + Math.sqrt(224 * N +
676)) / 56);
return (n - (int)n) == 0;
}
public static void main(String[] args)
{
int N = 30;
if (istriacontagonal(N))
{
System.out.print("Yes");
}
else
{
System.out.print("No");
}
}
}
|
Python3
import math;
def istriacontagonal(N):
n = (26 + math.sqrt(224 * N + 676)) // 56;
return (n - int(n)) == 0;
i = 30;
if (istriacontagonal(i)):
print("Yes");
else:
print("No");
|
C#
using System;
class GFG{
static bool istriacontagonal(int N)
{
float n = (float)((26 + Math.Sqrt(224 * N +
676)) / 56);
return (n - (int)n) == 0;
}
public static void Main(String[] args)
{
int N = 30;
if (istriacontagonal(N))
{
Console.Write("Yes");
}
else
{
Console.Write("No");
}
}
}
|
Javascript
<script>
function istriacontagonal( N)
{
let n = ((26 + Math.sqrt(224 * N +
676)) / 56);
return (n - parseInt(n)) == 0;
}
let N = 30;
if (istriacontagonal(N))
{
document.write("Yes");
}
else
{
document.write("No");
}
</script>
|
Time Complexity: O(log(n)), since sqrt() function has been used
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...