Program to calculate Electricity Bill

Given an integer U denoting the amount of KWh units of electricity consumed, the task is to calculate the electricity bill with the help of the below charges: 

• 1 to 100 units – 
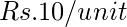
• 100 to 200 units – 
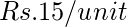
• 200 to 300 units – 
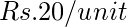
• above 300 units – 

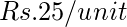
Examples:

Input: U = 250 
Output: 3500 
Explanation:
Charge for the first 100 units – 10*100 = 1000 
Charge for the 100 to 200 units – 15*100 = 1500 
Charge for the 200 to 250 units – 20*50 = 1000 
Total Electricity Bill = 1000 + 1500 + 1000 = 3500
Input: U = 95 
Output: 950 
Explanation:
Charge for the first 100 units – 10*95 = 950 
Total Electricity Bill = 950 

Approach 1: The idea is to identify the charge bar in which it falls and then calculate the bill according to the charges mentioned above. Below is the illustration of the steps: 

• Check units consumed is less than equal to the 100, If yes then the total electricity bill will be:
  

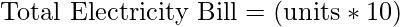
• Else if, check that units consumed is less than equal to the 200, if yes then total electricity bill will be:
  

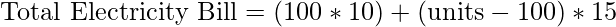
• Else if, check that units consumed is less than equal to the 300, if yes then total electricity bill will be:
  

• Else if, check that units consumed greater than 300, if yes then total electricity bill will be:
  

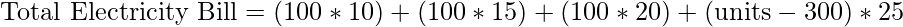
Below is the implementation of the above approach: 

C++

// C++ implementation to calculate the
// electricity bill
#include<bits/stdc++.h>
using namespace std;

// Function to calculate the
// electricity bill
int calculateBill(int units)
{

    // Condition to find the charges
    // bar in which the units consumed
    // is fall
    if (units <= 100)
    {
        return units * 10;
    }
    else if (units <= 200)
    {
        return (100 * 10) +
               (units - 100) * 15;
    }
    else if (units <= 300)
    {
        return (100 * 10) +
               (100 * 15) +
               (units - 200) * 20;
    }
    else if (units > 300)
    {
        return (100 * 10) +
               (100 * 15) +
               (100 * 20) +
               (units - 300) * 25;
    }
    return 0;
}

// Driver Code
int main()
{
    int units = 250;
    cout << calculateBill(units);
}

// This code is contributed by spp____

Java

// Java implementation to calculate the
// electricity bill

import java.util.*;

class ComputeElectricityBill {

    // Function to calculate the
    // electricity bill
    public static int calculateBill(int units)
    {

        // Condition to find the charges
        // bar in which the units consumed
        // is fall
        if (units <= 100) {
            return units * 10;
        }
        else if (units <= 200) {
            return (100 * 10)
                + (units - 100)
                      * 15;
        }
        else if (units <= 300) {
            return (100 * 10)
                + (100 * 15)
                + (units - 200)
                      * 20;
        }
        else if (units > 300) {
            return (100 * 10)
                + (100 * 15)
                + (100 * 20)
                + (units - 300)
                      * 25;
        }
        return 0;
    }

    // Driver Code
    public static void main(String args[])
    {
        int units = 250;

        System.out.println(
            calculateBill(units));
    }
}

Python3

# Python3 implementation to calculate the
# electricity bill

# Function to calculate the
# electricity bill
def calculateBill(units):

    # Condition to find the charges
    # bar in which the units consumed
    # is fall
    if (units <= 100):

        return units * 10;

    elif (units <= 200):

        return ((100 * 10) +
                (units - 100) * 15);

    elif (units <= 300):

        return ((100 * 10) +
                (100 * 15) +
                (units - 200) * 20);

    elif (units > 300):

        return ((100 * 10) +
                (100 * 15) +
                (100 * 20) +
                (units - 300) * 25);

    return 0;

# Driver Code
units = 250;
print(calculateBill(units));

# This code is contributed by Code_Mech

C#

// C# implementation to calculate the
// electricity bill
using System;

class ComputeElectricityBill{

// Function to calculate the
// electricity bill
public static int calculateBill(int units)
{

    // Condition to find the charges
    // bar in which the units consumed
    // is fall
    if (units <= 100)
    {
        return units * 10;
    }
    else if (units <= 200)
    {
        return (100 * 10) +
               (units - 100) * 15;
    }
    else if (units <= 300)
    {
        return (100 * 10) +
               (100 * 15) +
               (units - 200) * 20;
    }
    else if (units > 300)
    {
        return (100 * 10) +
               (100 * 15) +
               (100 * 20) +
               (units - 300) * 25;
    }
    return 0;
}

// Driver Code
public static void Main(String []args)
{
    int units = 250;

    Console.WriteLine(calculateBill(units));
}
}

// This code is contributed by spp____

Javascript

<script>

// Javascript implementation to calculate the
// electricity bill

// Function to calculate the
// electricity bill
function calculateBill(units)
{

    // Condition to find the charges
    // bar in which the units consumed
    // is fall
    if (units <= 100)
    {
        return units * 10;
    }
    else if (units <= 200)
    {
        return (100 * 10)
            + (units - 100)
                  * 15;
    }
    else if (units <= 300)
    {
        return (100 * 10)
            + (100 * 15)
            + (units - 200)
                  * 20;
    }
    else if (units > 300)
    {
        return (100 * 10)
            + (100 * 15)
            + (100 * 20)
            + (units - 300)
                  * 25;
    }
    return 0;
}

// Driver Code
var units = 250;

document.write(calculateBill(units));

// This code is contributed by Khushboogoyal499

</script>

Output

3500

Time Complexity: O(1)

Auxiliary Space: O(1)

Approach 2 : In this approach, we can use an array to store the different rate of charges and their respective range of units. This approach can make the code more readable and easier to maintain. Here’s how the code would look like:

C++

#include <bits/stdc++.h>
using namespace std;

const int n = 4;

// Function to calculate the electricity bill
int calculateBill(int units)
{
    int charges[n] = { 10, 15, 20, 25 };
    int range[n] = { 100, 100, 100, INT_MAX };
    int bill = 0;

    for (int i = 0; i < n; i++) {
        if (units <= range[i]) {
            bill += charges[i] * units;
            break;
        }
        else {
            bill += charges[i] * range[i];
            units -= range[i];
        }
    }
    return bill;
}

// Driver code
int main()
{
    int units = 250;
    cout << calculateBill(units);
    return 0;
}

Java

import java.util.*;

public class Main {

  public static final int n = 4;

  // Function to calculate the electricity bill
  public static int calculateBill(int units) {
    int[] charges = {10, 15, 20, 25};
    int[] range = {100, 100, 100, Integer.MAX_VALUE};
    int bill = 0;

    for (int i = 0; i < n; i++) {
      if (units <= range[i]) {
        bill += charges[i] * units;
        break;
      }
      else {
        bill += charges[i] * range[i];
        units -= range[i];
      }
    }
    return bill;
  }

  // Driver code
  public static void main(String[] args) {
    int units = 250;
    System.out.println(calculateBill(units));
  }
}

// This code is contributed by divyansh2212

Python3

import sys

MAX_INT = sys.maxsize
n = 4

# Function to calculate the electricity bill


def calculateBill(units):
    charges = [10, 15, 20, 25]
    # changed variable name from 'range' to 'range_'
    range_ = [100, 100, 100, MAX_INT]
    bill = 0

    for i in range(n):
        if units <= range_[i]:
            bill += charges[i] * units
            break
        else:
            bill += charges[i] * range_[i]
            units -= range_[i]

    return bill


# Driver code
units = 250
print(calculateBill(units))


# This code is contributed by shivhack999

C#

using System;

public class Program {
    const int n = 4;

    // Function to calculate the electricity bill
    static int CalculateBill(int units)
    {
        int[] charges = { 10, 15, 20, 25 };
        int[] range = { 100, 100, 100, int.MaxValue };
        int bill = 0;

        for (int i = 0; i < n; i++) {
            if (units <= range[i]) {
                bill += charges[i] * units;
                break;
            }
            else {
                bill += charges[i] * range[i];
                units -= range[i];
            }
        }
        return bill;
    }

    // Driver code
    public static void Main()
    {
        int units = 250;
        Console.WriteLine(CalculateBill(units));
    }
}
// This code is contributed by sarojmcy2e

Javascript

const n = 4;

// Function to calculate the electricity bill
function calculateBill(units) {
  const charges = [10, 15, 20, 25];
  const range = [100, 100, 100, Number.MAX_VALUE];
  let bill = 0;

  for (let i = 0; i < n; i++) {
    if (units <= range[i]) {
      bill += charges[i] * units;
      break;
    } else {
      bill += charges[i] * range[i];
      units -= range[i];
    }
  }
  return bill;
}

// Driver code
const units = 250;
console.log(calculateBill(units));
// This code is contributed by shiv1o43g

Output

3500

Time Complexity : The time complexity of the calculateBill function is O(n), where n is the number of ranges of units and their respective charges. This is because the function uses a for loop to iterate through the range and charges arrays, and for each iteration, it performs a constant amount of work (calculating the bill based on the units consumed).

Since n is a constant value, the time complexity can be considered as O(1) in the best-case scenario. The function takes a constant amount of time to run, regardless of the number of units consumed.

Auxiliary Space : The space complexity of this code is O(n), where n is the number of rate of charges. This is because the program uses two arrays, charges and range, both of which have a size of n elements. The arrays take up 2 * n * sizeof(int) bytes of memory. In this case, n = 4, so the total memory occupied by the arrays is 2 * 4 * sizeof(int).