Problem on Numbers
Last Updated :
14 Jun, 2022
Question 1 : Find the number of zeroes in 155!
Solution: Multiplication of 2×5 results into 10. So number of zeroes depend on the number of pairs of 2 and 5.
In any factorial, number of 5’s is lesser than the number of 2’s. So, we need to count the maximum power of 5 in 155!
[155/5] + [155/52] + [155/53]
=31 + 6 +1
=38
Hence, number of zeroes is 38.
Question 2: Find the number of factors in 8820.
Solution: Number of factors can be calculated by finding the prime factors.
8820= 22x32x51x72
Number of factors= (2 + 1)(2 + 1)(1 + 1)(2 + 1)
= 3 x 3 x 2 x 3
= 54
Question 3: Find the sum of all the factors of 576.
Solution: Prime factorization of 576= 26x32
Sum of all the factors= (20 + 21+ 22 + 23 + 24 + 25 + 26)*(30 + 31 + 32)
= 127*13
= 1651
Question 4: Find the product of all the factors of 600.
Solution: Prime factorization of 600= 23x31x52
Number of factors= (3+1)(1+1)(2+1)
= 4 * 2 * 3
= 24
Product of all the factors= (23x31x52)24/2
= (23x31x52)12
Question 5: Find the highest power of 126 which divides 366!.
Solution: 126=2×32x7
We need to check among 2, 3 and 7 which appears least number of times in 366!.
If we check factorial (1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 …….) then we got to know 7 appears less frequently than 2 and 3.
So, need to count only number of 7’s in 366!
[366/7] + [366/72] + [366/73]
=52 + 7 + 1
=60.
Question 6: Find the maximum value of n such that 671! is perfectly divisible by 45n.
Solution: Prime Factor of 45= 32x5
We will count the number of 32 and 5 in 671!, and which one is lesser in number would be the answer.
No of 3’s= 671/3 + 671/9 + 671/27 + 671/81 + 671/243
= 223 + 74 + 24 + 8 + 2
= 331
No of 32= 331/2 = 165
No of 5= 671/5 + 671/25 + 671/125 + 671/625
= 134 + 26 + 5 + 1
= 166
165 will be the answer because 32 is lower in number than 5.
Question 7 : Find the remainder (359 x 471)/11.
Solution: Divide individually both numbers and put remainder.
359/11 gives remainder 7
471/11 gives remainder 9
Put (7 x 9)/11 = 63/11 = 8 is the remainder.
Question 8 : Find the number of zeroes in the product:
11x22x33x44x55………555
Solution: Number of zeroes will be given by counting the number of 5’s.
55, 1010, 1515, 2020, 2525, 3030, 3535, 4040, 4545, 5050, 5555
The number of 5’s in these values
5 + 10 + 15 + 20 + 50 + 30 + 35 + 40 + 45 + 100 + 55 = 405
Question 9: Which of the following fraction is the smallest 7/6, 7/9, 4/5, 5/7 ?
Solution:
Step #1
Compare first two fractions 7/6 and 7/9
Cross multiply 63 > 42
7/9 fraction is smaller
Step #2 Compare the smaller one and the next fraction.
7/9 4/5
Cross multiply
35 < 36
7/9 is smaller
Step #3 Compare smaller one and next and repeat cross multiplication.
7/9 5/7
cross multiply
49 > 45
Here 5/7 is smallest fraction among all.
Question 10: If 19200 is divided by 20, the remainder is
Solution: We can write it as (20 – 1)200
Hence apply binomial theorem,
20200 (-1)0 + 20199 (-1)1 +………….. 200 (-1)200
Remainder always comes from the last term
200 (-1)200 / 20 = 1/20= 1
Question 11: If tripling a number and adding 10 to the result gives the same answer as multiplying the number by 4 and taking away 20 from the product, the number is :
Solution: Let x be the number
Acc. to question
3x + 10 = 4x – 20
x = 30
Question 12: Some students decided to go on campaign and planned to spend Rs 150 on eatables.Five friends did not turn up. As a consequence, each one of the remaining had to contribute Rs 5 extra. The number of students who attend campaign is
Solution: Let the number of students in the beginning is x.
Acc. to question
150/(x – 5) – 150/x = 5
150x – 150x + 750/ x(x – 5) = 5
x2 – 5x -150 = 0
x2 – 15x + 10x – 150 = 0
x(x – 15) + 10(x – 15) = 0
x = 15, -10
Hence the number of students in the beginning is 15.
Question 13: The value of (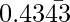 +
+ 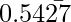 ) is
) is
Solution: It can be written as
(0.43434343….. + 0.54272727….)
After addition it will be
( 0.9770707070…) or (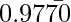 )
)
Question 14: Find 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56.
Solution: It can be written as
1/(2*3) + 1/(3*4) + 1/(4*5) + 1/(5*6) + 1/(6*7) + 1/(7*8)
= (1/2 – 1/3) + (1/3 – 1/4)+ (1/4 – 1/5) + (1/5 – 1/6) + (1/6 – 1/7)+ (1/7 – 1/8)
= 1/2 – 1/8
= (4 – 1)/8
= 3/8
Share your thoughts in the comments
Please Login to comment...