Number of stopping station problem

There are 12 intermediate stations between two places A and B. Find the number of ways in which a train can be made to stop at 4 of these intermediate stations so that no two stopping stations are consecutive?
Examples –

Input  : n = 12, s = 4
Output : 126

Input  : n = 16, s = 5
Output : 792

Explanation 1 :
Fix/remove of the four stops as fixed points and calculate in how many ways the other stations can be inserted between them, if you must have at least one station between stops. 

            A   x   x   x   x   x   x   x   x   B

Between these 8 non-halting stations we have 9 places and we select these 9 places as halt between these 8 stations. 
Therefore, answer should be 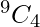= 126

Explanation 2 :
If you know about combinations about indistinguishable balls into distinguishable boxes, then you can simply use, 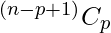. In this question, $n$ is number of stations and $p$ is number of stations on which you want to stop. Here stopping stations are as indistinguishable balls and non-stopping stations are as distinguishable boxes. 
Therefore, 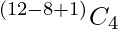= = 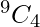126

Below is the code implementation of the solution:

C++

#include <stdio.h>
int stopping_station(int, int);

// function to calculate number
// of ways of selecting 'p' non consecutive
// stations out of 'n' stations
int stopping_station(int p, int n)
{

    int num = 1, dem = 1, s = p;

    // selecting 's' positions out of 'n-s+1'
    while (p != 1) {

        dem *= p;
        p--;
    }

    int t = n - s + 1;
    while (t != (n - 2 * s + 1)) {

        num *= t;
        t--;
    }

    if ((n - s + 1) >= s)
        printf("%d", num / dem);

    else

        // if conditions does not satisfy of combinatorics
        printf("not possible");
}

// driver code
int main()
{

    // n is total number of stations
    // s is no. of stopping stations
    int n, s;

    // arguments of function are
    // number of stopping station
    // and total number of stations
    stopping_station(4, 12);
}

Java

// Java code to calculate number
// of ways of selecting 'p' non
// consecutive stations out of
// 'n' stations

import java.io.*;
import java.util.*;

class GFG
{
    public static int stopping_station(int p, int n)
    {
        int num = 1, dem = 1, s = p;

        // selecting 's' positions out of 'n-s+1'
        while (p != 1)
        {
            dem *= p;
            p--;
        }

        int t = n - s + 1;
        while (t != (n - 2 * s + 1))
        {
            num *= t;
            t--;
        }

        if ((n - s + 1) >= s)
            System.out.print(num / dem);

        else
            // if conditions does not satisfy of combinatorics
            System.out.print("not possible");

        return 0;
    }

    public static void main (String[] args)
    {
        // n is total number of stations
        // s is no. of stopping stations
        int n, s;

        // arguments of function are
        // number of stopping station
        // and total number of stations
        stopping_station(4, 12);
    }
}
// ""This code is contributed by Mohit Gupta_OMG ""

Python3

# Python code to calculate number
# of ways of selecting 'p' non
# consecutive stations out of
# 'n' stations

def stopping_station( p, n):
    num = 1
    dem = 1
    s = p

    # selecting 's' positions
    # out of 'n-s+1'
    while p != 1:
        dem *= p
        p-=1

    t = n - s + 1
    while t != (n-2 * s + 1):
        num *= t
        t-=1
    if (n - s + 1) >= s:
        return int(num/dem)
    else:
        # if conditions does not
        # satisfy of combinatorics
        return -1

# driver code
num = stopping_station(4, 12)
if num != -1:
    print(num)
else:
    print("Not Possible")

# This code is contributed by "Abhishek Sharma 44"

C#

// C# code to calculate number
// of ways of selecting 'p' non
// consecutive stations out of
// 'n' stations
using System;

class GFG {

    public static int stopping_station(int p,
                                       int n)
    {
        int num = 1, dem = 1, s = p;

        // selecting 's' positions
        // out of 'n-s+1'
        while (p != 1)
        {
            dem *= p;
            p--;
        }

        int t = n - s + 1;
        while (t != (n - 2 * s + 1))
        {
            num *= t;
            t--;
        }

        if ((n - s + 1) >= s)
            Console.WriteLine(num / dem);

        // if conditions does not
        // satisfy of combinatorics
        else
          Console.WriteLine("Not possible");
        return 0;
    }

    // Driver Code
    public static void Main(String []args)
    {

        // arguments of function are
        // number of stopping station
        // and total number of stations
        stopping_station(4, 12);
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP code for Number of stopping
// station problem

// function to calculate number
// of ways of selecting 'p' non
// consecutive stations out of
// 'n' stations
function stopping_station(int $p, int $n)
{
    $num = 1;
    $dem = 1;
    $s = $p;

    // selecting 's' positions
    // out of 'n-s+1'
    while($p != 1)
    {

        $dem *= $p;
        $p--;
    }

    $t = $n - $s + 1;
    while($t != ($n - 2 * $s + 1))
    {
        $num *= $t;
        $t--;
    }

    if (($n - $s + 1) >= $s)
        echo $num / $dem;

    else

        // if conditions does not
        // satisfy of combinatorics
        echo "not possible";
}

    // Driver Code
    // n is total number of stations
    // s is no. of stopping stations
    $n; $s;

    // arguments of function are
    // number of stopping station
    // and total number of stations
    stopping_station(4, 12);

// This code is contributed by anuj_67.
?>

Javascript

<script>

// Javascript code to calculate number
// of ways of selecting 'p' non
// consecutive stations out of
// 'n' stations

    function stopping_station( p,  n)
    {
        var num = 1, dem = 1, s = p;

        // selecting 's' positions
        // out of 'n-s+1'
        while (p != 1)
        {
            dem *= p;
            p--;
        }

        var t = n - s + 1;
        while (t != (n - 2 * s + 1))
        {
            num *= t;
            t--;
        }

        if ((n - s + 1) >= s){
            document.write(num / dem);
         }

        // if conditions does not
        // satisfy of combinatorics
        else{
          document.write("Not possible");
          }
        return 0;
    }

    // Driver Code


        // arguments of function are
        // number of stopping station
        // and total number of stations
        stopping_station(4, 12);

</script>

Output :

126

Time Complexity: O(s)
Auxiliary Space: O(1)