Probability such that two subset contains same number of elements
Last Updated :
05 May, 2021
Given a set containing N elements. If two subset X and Y picked then find the probability that both of them contains the same number of elements.
Examples:
Input: 4
Output: 35/128
Input: 2
Output: 3/8
Approach:
Let’s choose a subset X that has r number of elements then Y must contain r number of elements. A subset can have minimum 0 elements and maximum N elements.
Total number of subsets of a set contains N number of elements is
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
, Total possible way to choose
X and
Y simultaneously will be
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
= *** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
= *** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
.
Let,
P = Total possible way to choose
X and
Y such that both have the same number of elements.
Then P =
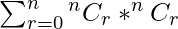
=
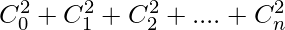
=

So the required probability will be
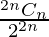
.
Below is the implementation of the above Approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k)
{
int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
int power(int x, unsigned int y)
{
int res = 1;
while (y > 0) {
if (y & 1)
res = res * x;
y = y >> 1;
x = x * x;
}
return res;
}
void FindProbability(int n)
{
int up = binomialCoeff(2 * n, n);
int down = power(2, 2 * n);
int g = __gcd(up, down);
up /= g, down /= g;
cout << up << "/" << down << endl;
}
int main()
{
int N = 8;
FindProbability(N);
return 0;
}
|
Java
class GFG
{
static int binomialCoeff(int n, int k)
{
int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int power(int x, int y)
{
int res = 1;
while (y > 0)
{
if ((y & 1) == 1)
res = res * x;
y = y >> 1;
x = x * x;
}
return res;
}
static int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
static void FindProbability(int n)
{
int up = binomialCoeff(2 * n, n);
int down = power(2, 2 * n);
int g = gcd(up, down);
up /= g;
down /= g;
System.out.println(up + "/" + down);
}
public static void main (String[] args)
{
int N = 8;
FindProbability(N);
}
}
|
Python3
import math
def binomialCoeff(n, k):
res = 1
if (k > n - k):
k = n - k
for i in range(0, k):
res = res * (n - i)
res = res // (i + 1)
return res
def power(x, y):
res = 1
while (y > 0):
if (y & 1):
res = res * x
y = y // 2
x = x * x
return res
def FindProbability(n):
up = binomialCoeff(2 * n, n)
down = power(2, 2 * n)
g = math.gcd(up,down)
up = up // g
down = down // g
print(up, "/", down)
N = 8
FindProbability(N)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int binomialCoeff(int n, int k)
{
int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i)
{
res *= (n - i);
res /= (i + 1);
}
return res;
}
static int power(int x, int y)
{
int res = 1;
while (y > 0)
{
if ((y & 1) == 1)
res = res * x;
y = y >> 1;
x = x * x;
}
return res;
}
static int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
static void FindProbability(int n)
{
int up = binomialCoeff(2 * n, n);
int down = power(2, 2 * n);
int g = gcd(up, down);
up /= g;
down /= g;
Console.WriteLine(up + "/" + down);
}
public static void Main (String[] args)
{
int N = 8;
FindProbability(N);
}
}
|
Javascript
<script>
function binomialCoeff(n, k)
{
let res = 1;
if (k > n - k)
k = n - k;
for (let i = 0; i < k; ++i) {
res *= (n - i);
res = parseInt(res / (i + 1));
}
return res;
}
function power(x, y)
{
let res = 1;
while (y > 0) {
if (y & 1)
res = res * x;
y = y >> 1;
x = x * x;
}
return res;
}
function gcd(a, b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
function FindProbability(n)
{
let up = binomialCoeff(2 * n, n);
let down = power(2, 2 * n);
let g = gcd(up, down);
up = parseInt(up / g), down = parseInt(down / g);
document.write(up + "/" + down + "<br>");
}
let N = 8;
FindProbability(N);
</script>
|
Share your thoughts in the comments
Please Login to comment...