Print all subsequences of a string | Iterative Method
Last Updated :
20 Feb, 2023
Given a string s, print all possible subsequences of the given string in an iterative manner. We have already discussed Recursive method to print all subsequences of a string.
Examples:
Input : abc
Output : a, b, c, ab, ac, bc, abc
Input : aab
Output : a, b, aa, ab, aab
Approach 1 :
Here, we discuss much easier and simpler iterative approach which is similar to Power Set. We use bit pattern from binary representation of 1 to 2^length(s) – 1.
input = “abc”
Binary representation to consider 1 to (2^3-1), i.e 1 to 7.
Start from left (MSB) to right (LSB) of binary representation and append characters from input string which corresponds to bit value 1 in binary representation to Final subsequence string sub.
Example:
001 => abc . Only c corresponds to bit 1. So, subsequence = c.
101 => abc . a and c corresponds to bit 1. So, subsequence = ac.
binary_representation (1) = 001 => c
binary_representation (2) = 010 => b
binary_representation (3) = 011 => bc
binary_representation (4) = 100 => a
binary_representation (5) = 101 => ac
binary_representation (6) = 110 => ab
binary_representation (7) = 111 => abc
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string subsequence(string s, int binary, int len)
{
string sub = "";
for (int j = 0; j < len; j++)
if (binary & (1 << j))
sub += s[j];
return sub;
}
void possibleSubsequences(string s){
map<int, set<string> > sorted_subsequence;
int len = s.size();
int limit = pow(2, len);
for (int i = 1; i <= limit - 1; i++) {
string sub = subsequence(s, i, len);
sorted_subsequence[sub.length()].insert(sub);
}
for (auto it : sorted_subsequence) {
cout << "Subsequences of length = "
<< it.first << " are:" << endl;
for (auto ii : it.second)
cout << ii << " ";
cout << endl;
}
}
int main()
{
string s = "aabc";
possibleSubsequences(s);
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.SortedMap;
import java.util.TreeMap;
class Graph{
static String subsequence(String s,
int binary,
int len)
{
String sub = "";
for(int j = 0; j < len; j++)
if ((binary & (1 << j)) != 0)
sub += s.charAt(j);
return sub;
}
static void possibleSubsequences(String s)
{
SortedMap<Integer,
HashSet<String>> sorted_subsequence = new TreeMap<Integer,
HashSet<String>>();
int len = s.length();
int limit = (int) Math.pow(2, len);
for(int i = 1; i <= limit - 1; i++)
{
String sub = subsequence(s, i, len);
if (!sorted_subsequence.containsKey(sub.length()))
sorted_subsequence.put(
sub.length(), new HashSet<>());
sorted_subsequence.get(
sub.length()).add(sub);
}
for(Map.Entry<Integer,
HashSet<String>> it : sorted_subsequence.entrySet())
{
System.out.println("Subsequences of length = " +
it.getKey() + " are:");
for(String ii : it.getValue())
System.out.print(ii + " ");
System.out.println();
}
}
public static void main(String[] args)
{
String s = "aabc";
possibleSubsequences(s);
}
}
|
Python3
def subsequence(s, binary, length):
sub = ""
for j in range(length):
if (binary & (1 << j)):
sub += s[j]
return sub
def possibleSubsequences(s):
sorted_subsequence = {}
length = len(s)
limit = 2 ** length
for i in range(1, limit):
sub = subsequence(s, i, length)
if len(sub) in sorted_subsequence.keys():
sorted_subsequence[len(sub)] = \
tuple(list(sorted_subsequence[len(sub)]) + [sub])
else:
sorted_subsequence[len(sub)] = [sub]
for it in sorted_subsequence:
print("Subsequences of length =", it, "are:")
for ii in sorted(set(sorted_subsequence[it])):
print(ii, end = ' ')
print()
s = "aabc"
possibleSubsequences(s)
|
C#
using System;
using System.Collections.Generic;
class Graph {
static string subsequence(string s, int binary, int len)
{
string sub = "";
for (int j = 0; j < len; j++)
if ((binary & (1 << j)) != 0)
sub += s[j];
return sub;
}
static void possibleSubsequences(string s)
{
SortedDictionary<int, HashSet<string> >
sorted_subsequence
= new SortedDictionary<int, HashSet<string> >();
int len = s.Length;
int limit = (int)Math.Pow(2, len);
for (int i = 1; i <= limit - 1; i++) {
string sub = subsequence(s, i, len);
if (!sorted_subsequence.ContainsKey(sub.Length))
sorted_subsequence[sub.Length]
= new HashSet<string>();
sorted_subsequence[sub.Length].Add(sub);
}
foreach(var it in sorted_subsequence)
{
Console.WriteLine("Subsequences of length = "
+ it.Key + " are:");
foreach(String ii in it.Value)
Console.Write(ii + " ");
Console.WriteLine();
}
}
public static void Main(string[] args)
{
string s = "aabc";
possibleSubsequences(s);
}
}
|
Javascript
<script>
function subsequence(s, binary, len)
{
let sub = "";
for(let j = 0; j < len; j++)
if (binary & (1 << j))
sub += s[j];
return sub;
}
function possibleSubsequences(s)
{
let sorted_subsequence = new Map();
let len = s.length;
let limit = Math.pow(2, len);
for(let i = 1; i <= limit - 1; i++)
{
let sub = subsequence(s, i, len);
if (!sorted_subsequence.has(sub.length))
sorted_subsequence.set(sub.length, new Set());
sorted_subsequence.get(sub.length).add(sub);
}
for(let it of sorted_subsequence)
{
document.write("Subsequences of length = " +
it[0] + " are:" + "<br>");
for(let ii of it[1])
document.write(ii + " ");
document.write("<br>");
}
}
let s = "aabc";
possibleSubsequences(s);
</script>
|
OutputSubsequences of length = 1 are:
a b c
Subsequences of length = 2 are:
aa ab ac bc
Subsequences of length = 3 are:
aab aac abc
Subsequences of length = 4 are:
aabc
Time Complexity : O(2^n), where n is length of string to find subsequences and n is length of binary string.
Space Complexity: O(1)
Approach 2 :
Approach is to get the position of rightmost set bit and reset that bit after appending corresponding character from given string to the subsequence and will repeat the same thing till corresponding binary pattern has no set bits.
If input is s = “abc”
Binary representation to consider 1 to (2^3-1), i.e 1 to 7.
001 => abc . Only c corresponds to bit 1. So, subsequence = c
101 => abc . a and c corresponds to bit 1. So, subsequence = ac.
Let us use Binary representation of 5, i.e 101.
Rightmost bit is at position 1, append character at beginning of sub = c ,reset position 1 => 100
Rightmost bit is at position 3, append character at beginning of sub = ac ,reset position 3 => 000
As now we have no set bit left, we stop computing subsequence.
Example:
binary_representation (1) = 001 => c
binary_representation (2) = 010 => b
binary_representation (3) = 011 => bc
binary_representation (4) = 100 => a
binary_representation (5) = 101 => ac
binary_representation (6) = 110 => ab
binary_representation (7) = 111 => abc
Below is the implementation of above approach :
C++
#include <bits/stdc++.h>
using namespace std;
string subsequence(string s, int binary)
{
string sub = "";
int pos;
while(binary>0)
{
pos=log2(binary&-binary)+1;
sub=s[pos-1]+sub;
binary= (binary & ~(1 << (pos-1)));
}
reverse(sub.begin(),sub.end());
return sub;
}
void possibleSubsequences(string s){
map<int, set<string> > sorted_subsequence;
int len = s.size();
int limit = pow(2, len);
for (int i = 1; i <= limit - 1; i++) {
string sub = subsequence(s, i);
sorted_subsequence[sub.length()].insert(sub);
}
for (auto it : sorted_subsequence) {
cout << "Subsequences of length = "
<< it.first << " are:" << endl;
for (auto ii : it.second)
cout << ii << " ";
cout << endl;
}
}
int main()
{
string s = "aabc";
possibleSubsequences(s);
return 0;
}
|
Java
import java.util.*;
public class GFG {
public static String subsequence(String s, int binary) {
String sub = "";
int pos;
while (binary > 0) {
pos = (int) (Math.log(binary & -binary) / Math.log(2)) + 1;
sub = s.charAt(pos - 1) + sub;
binary = (binary & ~(1 << (pos - 1)));
}
sub = new StringBuilder(sub).reverse().toString();
return sub;
}
public static void possibleSubsequences(String s) {
Map<Integer, Set<String>> sortedSubsequence = new HashMap<>();
int len = s.length();
int limit = (int) Math.pow(2, len);
for (int i = 1; i <= limit - 1; i++) {
String sub = subsequence(s, i);
sortedSubsequence.computeIfAbsent(sub.length(), k -> new TreeSet<>()).add(sub);
}
for (Map.Entry<Integer, Set<String>> it : sortedSubsequence.entrySet()) {
System.out.println("Subsequences of length = " + it.getKey() + " are:");
for (String ii : it.getValue())
System.out.print(ii + " ");
System.out.println();
}
}
public static void main(String[] args) {
String s = "aabc";
possibleSubsequences(s);
}
}
|
Python3
from math import log2, floor
def subsequence(s, binary):
sub = ""
while(binary > 0):
pos=floor(log2(binary&-binary) + 1)
sub = s[pos - 1] + sub
binary= (binary & ~(1 << (pos - 1)))
sub = sub[::-1]
return sub
def possibleSubsequences(s):
sorted_subsequence = {}
length = len(s)
limit = 2 ** length
for i in range(1, limit):
sub = subsequence(s, i)
if len(sub) in sorted_subsequence.keys():
sorted_subsequence[len(sub)] = \
tuple(list(sorted_subsequence[len(sub)]) + [sub])
else:
sorted_subsequence[len(sub)] = [sub]
for it in sorted_subsequence:
print("Subsequences of length =", it, "are:")
for ii in sorted(set(sorted_subsequence[it])):
print(ii, end = ' ')
print()
s = "aabc"
possibleSubsequences(s)
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class GFG
{
static string subsequence(string s, int binary)
{
string sub = "";
while (binary > 0) {
var pos = (int)Math.Floor(
Math.Log(binary & (-binary))
/ Math.Log(2))
+ 1;
sub = s[pos - 1] + sub;
binary = (binary & ~(1 << (pos - 1)));
}
char[] charArray = sub.ToCharArray();
Array.Reverse(charArray);
return new string(charArray);
}
static void possibleSubsequences(string s)
{
Dictionary<int, HashSet<string> > sorted_subsequence
= new Dictionary<int, HashSet<string> >();
int length = s.Length;
int limit = (int)Math.Pow(2, length);
for (int i = 1; i < limit; i++) {
string sub = subsequence(s, i);
if (sorted_subsequence.ContainsKey(
sub.Length)) {
sorted_subsequence[sub.Length].Add(sub);
}
else {
sorted_subsequence[sub.Length]
= new HashSet<string>();
sorted_subsequence[sub.Length].Add(sub);
}
}
foreach(var it in sorted_subsequence)
{
Console.WriteLine("Subsequences of length = "
+ it.Key + " are:");
var arr = (it.Value).ToArray();
Array.Sort(arr);
for (int i = 0; i < arr.Length; i++) {
Console.Write(arr[i] + " ");
}
Console.WriteLine();
}
}
public static void Main(string[] args)
{
string s = "aabc";
possibleSubsequences(s);
}
}
|
Javascript
function subsequence(s, binary)
{
var sub = "";
while(binary > 0)
{
var pos= Math.floor(Math.log2(binary&-binary) + 1);
sub = s[pos - 1] + sub;
binary= (binary & ~(1 << (pos - 1)));
}
sub = sub.split("");
sub = sub.reverse();
return sub.join("");
}
function possibleSubsequences(s)
{
var sorted_subsequence = {};
var length = s.length;
var limit = 2 ** length;
for (var i = 1; i < limit; i++)
{
var sub = subsequence(s, i);
if (sorted_subsequence.hasOwnProperty(sub.length))
{
sorted_subsequence[sub.length].push(sub);
}
else
sorted_subsequence[sub.length] = [sub];
}
for (const it in sorted_subsequence)
{
console.log("Subsequences of length =", it, "are:");
var arr = sorted_subsequence[it];
arr.sort();
var set = new Set(arr);
for (const ii of set)
process.stdout.write(ii + " ");
console.log()
}
}
var s = "aabc";
possibleSubsequences(s);
|
OutputSubsequences of length = 1 are:
a b c
Subsequences of length = 2 are:
aa ab ac bc
Subsequences of length = 3 are:
aab aac abc
Subsequences of length = 4 are:
aabc
Time Complexity: 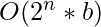 , where n is the length of string to find subsequence and b is the number of set bits in binary string.
, where n is the length of string to find subsequence and b is the number of set bits in binary string.
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...