Pair with given sum and maximum shortest distance from end
Last Updated :
25 Jul, 2022
Given an array of N integers and an integer K, pick two distinct elements whose sum is K and find the maximum shortest distance of the picked elements from the endpoints.
Examples:
Input : a[] = {2, 4, 3, 2, 1}
k = 5.
Output : 2
Explanation:
Select the pair(4, 1).
Shortest distance of 4 from ends = 2
Shortest distance of 1 from ends = 1
Hence, answer is max(2, 1) = 2
Input : a[] = {2, 4, 1, 9, 5}
k = 3
Output : 3
Explanation:
Select the pair (2, 1)
Shortest distance of 2 from ends = 1
Shortest distance of 1 from ends = 3
Hence, answer is max(1, 3) = 3.
Note: The distance of end elements from ends is 1 and not 0.
Naive approach: The approach is to run two loops and in inner loop check if two elements are making a pair with sum k. If yes, then make answer as maximum of the shortest distances of two elements, compare it with the previous pair’s answer and make answer as minimum of these two. When the loop ends we get the desired output.
Efficient Approach: Clearly, Shortest distance is the distance from left end and distance from right end i.e, 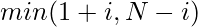 . Let us denote shortest distance of i-th element as
. Let us denote shortest distance of i-th element as 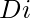 . There is another case where an element in the selected pair is repeated then select minimum of all the shortest distances of occurrences of that element. Run a loop and store shortest distance of all the array elements in another array(let it be
. There is another case where an element in the selected pair is repeated then select minimum of all the shortest distances of occurrences of that element. Run a loop and store shortest distance of all the array elements in another array(let it be ![Rendered by QuickLaTeX.com D[]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfd2ca95650c392521f9b4292c6741d1_l3.png) ). Now, we got shortest distances of all the elements.
). Now, we got shortest distances of all the elements.
Run a for loop. If the picked element is x, then the other element should be k-x. Update the ans with ![Rendered by QuickLaTeX.com max(D[x], D[k-x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b63514b47898d1c2af3c1675456f51cb_l3.png) and at every update, select the minimum of previous and present answer. If k-x is not in the array, then
and at every update, select the minimum of previous and present answer. If k-x is not in the array, then ![Rendered by QuickLaTeX.com D[k-x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-254b61146048ad4393a0be8d224b49a2_l3.png) will be INFINITE, which will be initialized already.
will be INFINITE, which will be initialized already.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int find_maximum(int a[], int n, int k)
{
unordered_map<int, int> b;
for (int i = 0; i < n; i++) {
int x = a[i];
int d = min(1 + i, n - i);
if (b.find(x) == b.end())
b[x] = d;
else
b[x] = min(d, b[x]);
}
int ans = INT_MAX;
for (int i = 0; i < n; i++) {
int x = a[i];
if (x != k - x && b.find(k - x) != b.end())
ans = min(max(b[x], b[k - x]), ans);
}
return ans;
}
int main()
{
int a[] = { 3, 5, 8, 6, 7 };
int K = 11;
int n = sizeof(a) / sizeof(a[0]);
cout << find_maximum(a, n, K) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void makePermutation(int []a, int n)
{
HashMap<Integer,
Integer> count = new HashMap<Integer,
Integer>();
for (int i = 0; i < n; i++)
{
if(count.containsKey(a[i]))
{
count.put(a[i], count.get(a[i]) + 1);
}
else
{
count.put(a[i], 1);
}
}
}
static int find_maximum(int a[], int n, int k)
{
HashMap<Integer,
Integer> b = new HashMap<Integer,
Integer>();
for (int i = 0; i < n; i++)
{
int x = a[i];
int d = Math.min(1 + i, n - i);
if (!b.containsKey(x))
b.put(x, d);
else
{
b. put(x, Math.min(d, b.get(x)));
}
}
int ans = Integer.MAX_VALUE;
for (int i = 0; i < n; i++)
{
int x = a[i];
if (x != k - x && b.containsKey(k - x))
ans = Math.min(Math.max(b.get(x),
b.get(k - x)), ans);
}
return ans;
}
public static void main(String[] args)
{
int a[] = { 3, 5, 8, 6, 7 };
int K = 11;
int n = a.length;
System.out.println(find_maximum(a, n, K));
}
}
|
Python3
def find_maximum(a, n, k):
b = dict()
for i in range(n):
x = a[i]
d = min(1 + i, n - i)
if x not in b.keys():
b[x] = d
else:
b[x] = min(d, b[x])
ans = 10**9
for i in range(n):
x = a[i]
if (x != (k - x) and (k - x) in b.keys()):
ans = min(max(b[x], b[k - x]), ans)
return ans
a = [3, 5, 8, 6, 7]
K = 11
n = len(a)
print(find_maximum(a, n, K))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void makePermutation(int []a, int n)
{
Dictionary<int,
int> count = new Dictionary<int,
int>();
for (int i = 0; i < n; i++)
{
if(count.ContainsKey(a[i]))
{
count[a[i]] = count[a[i]] + 1;
}
else
{
count.Add(a[i], 1);
}
}
}
static int find_maximum(int []a, int n, int k)
{
Dictionary<int,
int> b = new Dictionary<int,
int>();
for (int i = 0; i < n; i++)
{
int x = a[i];
int d = Math.Min(1 + i, n - i);
if (!b.ContainsKey(x))
b.Add(x, d);
else
{
b[x] = Math.Min(d, b[x]);
}
}
int ans = int.MaxValue;
for (int i = 0; i < n; i++)
{
int x = a[i];
if (x != k - x && b.ContainsKey(k - x))
ans = Math.Min(Math.Max(b[x],
b[k - x]), ans);
}
return ans;
}
public static void Main(String[] args)
{
int []a = { 3, 5, 8, 6, 7 };
int K = 11;
int n = a.Length;
Console.WriteLine(find_maximum(a, n, K));
}
}
|
Javascript
<script>
function makePermutation(a,n)
{
let count = new Map();
for (let i = 0; i < n; i++)
{
if(count.has(a[i]))
{
count.set(a[i], count.get(a[i]) + 1);
}
else
{
count.set(a[i], 1);
}
}
}
function find_maximum(a,n,k)
{
let b = new Map();
for (let i = 0; i < n; i++)
{
let x = a[i];
let d = Math.min(1 + i, n - i);
if (!b.has(x))
b.set(x, d);
else
{
b. set(x, Math.min(d, b.get(x)));
}
}
let ans = Number.MAX_VALUE;
for (let i = 0; i < n; i++)
{
let x = a[i];
if (x != k - x && b.has(k - x))
ans = Math.min(Math.max(b.get(x),
b.get(k - x)), ans);
}
return ans;
}
let a=[3, 5, 8, 6, 7 ];
let K = 11;
let n = a.length;
document.write(find_maximum(a, n, K));
</script>
|
Output:
2
Time Complexity : O(n)
Auxiliary Space : O(n)
Share your thoughts in the comments
Please Login to comment...