Print all Prime Quadruplet of a number less than it

Given a positive integer n, print every Prime Quadruplet below .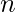
Prime quadruplet: In mathematics, Prime Quadruplet is a set of four primes of the form {p, p+2, p+6, p+8 }.
Example : 

Input : N = 15
Output : 5  7  11  13
                           
Input : N = 20
Output :  5  7  11  13
           11 13 17  19

A Simple solution to generate all Prime quadruplets up to n is to traverse all positive integer ‘i’ from i=1 to n and check if i, i+2, i+6 and i+8 are primes or not.
An Efficient Solution is to use Sieve Of Eratosthenes to pre-compute all prime numbers in an array in the certain range. 
Approach: 

1. Pre-Compute Prime numbers using Sieve Of Eratosthenes ( refer this )
2. Traverse from i=0 to n-7 and check if i, i+2, i+6 and i+8 are also prime or not. 
3. If yes, Then print i, i+2, i+6, i+8, 
   Otherwise increment i and check again

Below is the implementation of above idea: 

C++

// CPP Program to print prime quadruplet

#include <bits/stdc++.h>
using namespace std;

#define MAX 100000

bool prime[MAX];

// Utility function to generate prime numbers
void sieve()
{
    // Sieve Of Eratosthenes for generating
    // prime number.
    memset(prime, true, sizeof(prime));

    for (int p = 2; p * p < MAX; p++) {

        // If prime[p] is not changed,
        // then it is a prime
        if (prime[p] == true) {

            // Update all multiples of p
            for (int i = p * 2; i < MAX; i += p)
                prime[i] = false;
        }
    }
}

// Function to print Prime quadruplet
void printPrimeQuad(int n)
{

    for (int i = 0; i < n - 7; i++) {

        if (prime[i] && prime[i + 2] && prime[i + 6]
            && prime[i + 8]) {

            cout << i << " " << i + 2 << " " << i + 6
                 << " " << i + 8 << "\n";
        }
    }
}

// Driver Code
int main()
{
    sieve();
    int n = 20;

    printPrimeQuad(20);

    return 0;
}

Java

// Java code to print prime Quarduplet in a range
import java.util.Arrays;
import java.util.Collections;

class GFG {

    static final int MAX = 1000000;
    static boolean[] prime = new boolean[MAX];

    // utility function to generate prime number
    public static void sieve()
    {
        // Sieve Of Eratosthenes for generating
        // prime number.

        // memset(prime, true, sizeof(prime));
        Arrays.fill(prime, true);

        for (int p = 2; p * p < MAX; p++) {

            // If prime[p] is not changed,
            // then it is a prime
            if (prime[p] == true) {

                // Update all multiples of p
                for (int i = p * 2; i < MAX; i += p)
                    prime[i] = false;
            }
        }
    }

    // function to print prime Quadruplet
    static void printPrimeQuad(int n)
    {
        for (int i = 0; i < n - 7; i++) {

            if (prime[i] && prime[i + 2] && prime[i + 6]
                && prime[i + 8]) {

                System.out.println(i + " " + (i + 2) + " "
                                   + (i + 6) + " " + (i + 8));
            }
        }
    }

    // Driver Code
    public static void main(String[] args)
    {
        int n = 20;

        sieve();

        printPrimeQuad(n);
    }
}

Python3

# Python3 Program to print
# prime quadruplet

# from math lib import sqrt method
from math import sqrt

MAX = 100000

# Sieve Of Eratosthenes for generating
# prime number.
prime = [True] * MAX

# Utility function to generate
# prime numbers
def sieve() :

    for p in range(2, int(sqrt(MAX)) + 1) :

        # If prime[p] is not changed,
        # then it is a prime
        if prime[p] == True :

            # Update all multiples of p
            for i in range(p * 2 , MAX, p) :
                prime[i] = False


# Function to print Prime quadruplet
def printPrimeQuad(n) :

    for i in range(n - 7) :

        if ( prime[i] and prime[i + 2] and prime[i + 6]
            and prime[i + 8]) :

            print(i,i + 2,i + 6,i + 8)


# Driver code
if __name__ == "__main__" :

    sieve()
    n = 20

    printPrimeQuad(20)

# This code is contributed by
# ANKITRAI1

C#

// C# code to print prime Quarduplet in a range

using System;

class GFG {

     const int MAX = 1000000;
    static bool[] prime = new bool[MAX];

    // utility function to generate prime number
    public static void sieve()
    {
        // Sieve Of Eratosthenes for generating
        // prime number.

        // memset(prime, true, sizeof(prime));
        for(int i=0;i<MAX;i++) prime[i]=true;

        for (int p = 2; p * p < MAX; p++) {

            // If prime[p] is not changed,
            // then it is a prime
            if (prime[p] == true) {

                // Update all multiples of p
                for (int i = p * 2; i < MAX; i += p)
                    prime[i] = false;
            }
        }
    }

    // function to print prime Quadruplet
    static void printPrimeQuad(int n)
    {
        for (int i = 0; i < n - 7; i++) {

            if (prime[i] && prime[i + 2] && prime[i + 6]
                && prime[i + 8]) {

                Console.WriteLine(i + " " + (i + 2) + " "
                                   + (i + 6) + " " + (i + 8));
            }
        }
    }

    // Driver Code
    public static void Main()
    {
        int n = 20;

        sieve();

        printPrimeQuad(n);
    }
}

PHP

<?php
// PHP Program to print prime quadruplet
$MAX = 100000;

// Sieve Of Eratosthenes for generating
// prime number.
$prime = array_fill(0, $MAX, true);

// Utility function to generate
// prime numbers
function sieve()
{
    global $MAX, $prime;

    for ($p = 2; $p * $p < $MAX; $p++)
    {

        // If prime[p] is not changed,
        // then it is a prime
        if ($prime[$p] == true)
        {

            // Update all multiples of p
            for ($i = $p * 2; $i < $MAX; $i += $p)
                $prime[$i] = false;
        }
    }
}

// Function to print Prime quadruplet
function printPrimeQuad($n)
{
    global $MAX, $prime;
    for ($i = 0; $i < $n - 7; $i++)
    {

        if ($prime[$i] && $prime[$i + 2] &&
            $prime[$i + 6] && $prime[$i + 8])
        {

            echo $i . " " . ($i + 2) . " " .
                ($i + 6) . " " . ($i + 8) . "\n";
        }
    }
}

// Driver Code
sieve();
$n = 20;

printPrimeQuad(20);

// This code is contributed by mits
?>

Javascript

<script>

// Javascript Program to print prime quadruplet

var MAX = 100000;

var prime = Array(MAX).fill(true);

// Utility function to generate prime numbers
function sieve()
{
    // Sieve Of Eratosthenes for generating
    // prime number.

    for (var p = 2; p * p < MAX; p++) {

        // If prime[p] is not changed,
        // then it is a prime
        if (prime[p] == true) {

            // Update all multiples of p
            for (var i = p * 2; i < MAX; i += p)
                prime[i] = false;
        }
    }
}

// Function to print Prime quadruplet
function printPrimeQuad(n)
{

    for (var i = 0; i < n - 7; i++) {

        if (prime[i] && prime[i + 2] && prime[i + 6]
            && prime[i + 8]) {

            document.write( i + " " + (i + 2) + " "
            + (i + 6) + " " + (i + 8) + "<br>");
        }
    }
}

// Driver Code
sieve();
var n = 20;
printPrimeQuad(20);

</script>

Output:

5 7 11 13
11 13 17 19

Time Complexity: O(n * (MAX)^3/2)

Auxiliary Space: O(MAX)

See Also: 

• Twin Prime
• Prime Triplet
• Sexy Prime
• Cousin Prime
• Balanced Prime