Permutations of n things taken r at a time with k things together
Last Updated :
04 Aug, 2022
Given n, r, and K. The task is to find the number of permutations of 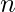 different things taken
different things taken 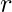 at a time such that
at a time such that 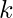 specific things always occur together.
specific things always occur together.
Examples:
Input : n = 8, r = 5, k = 2
Output : 960
Input : n = 6, r = 2, k = 2
Output : 2
Approach:
- A bundle of
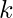 specific things can be put in r places in (r – k + 1) ways .
specific things can be put in r places in (r – k + 1) ways . - k specific things in the bundle can be arranged themselves into k! ways.
- Now (n – k) things will be arranged in (r – k) places in
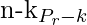 ways.
ways.
Thus, using the fundamental principle of counting, the required number of permutations will be:
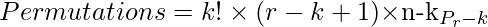
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
int npr(int n, int r)
{
int pnr = factorial(n) / factorial(n - r);
return pnr;
}
int countPermutations(int n, int r, int k)
{
return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
int main()
{
int n = 8;
int r = 5;
int k = 2;
cout << countPermutations(n, r, k);
return 0;
}
|
Java
class GFG{
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
static int npr(int n, int r)
{
int pnr = factorial(n) / factorial(n - r);
return pnr;
}
static int countPermutations(int n, int r, int k)
{
return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
public static void main(String[] args)
{
int n = 8;
int r = 5;
int k = 2;
System.out.println(countPermutations(n, r, k));
}
}
|
Python3
def factorial(n):
fact = 1;
for i in range(2,n+1):
fact = fact * i;
return fact;
def npr(n, r):
pnr = factorial(n) / factorial(n - r);
return pnr;
def countPermutations(n, r, k):
return int(factorial(k) * (r - k + 1) * npr(n - k, r - k));
n = 8;
r = 5;
k = 2;
print(countPermutations(n, r, k));
|
C#
using System;
class GFG
{
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
static int npr(int n, int r)
{
int pnr = factorial(n) /
factorial(n - r);
return pnr;
}
static int countPermutations(int n,
int r, int k)
{
return factorial(k) * (r - k + 1) *
npr(n - k, r - k);
}
static void Main()
{
int n = 8;
int r = 5;
int k = 2;
Console.WriteLine(countPermutations(n, r, k));
}
}
|
PHP
<?php
function factorial($n)
{
$fact = 1;
for ($i = 2; $i <= $n; $i++)
$fact = $fact * $i;
return $fact;
}
function npr($n, $r)
{
$pnr = factorial($n) /
factorial($n - $r);
return $pnr;
}
function countPermutations($n, $r, $k)
{
return factorial($k) * ($r - $k + 1) *
npr($n - $k, $r - $k);
}
$n = 8;
$r = 5;
$k = 2;
echo countPermutations($n, $r, $k);
?>
|
Javascript
<script>
function factorial(n)
{
let fact = 1;
for (let i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
function npr(n, r)
{
let pnr = Math.floor(factorial(n) / factorial(n - r));
return pnr;
}
function countPermutations(n, r, k)
{
return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
let n = 8;
let r = 5;
let k = 2;
document.write(countPermutations(n, r, k));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...