Permutations of n things taken all at a time with m things never come together
Last Updated :
26 Feb, 2023
Given n and m, the task is to find the number of permutations of n distinct things taking them all at a time such that m particular things never come together.
Examples:
Input : 7, 3
Output : 420
Input : 9, 2
Output : 282240
Approach:
Derivation of the formula –
Total number of arrangements possible using n distinct objects taking all at a time = 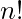
Number of arrangements of n distinct things taking all at a time, when m particular things always come together, is 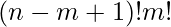
Hence, the number of permutations of 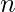 distinct things taking all at a time, when
distinct things taking all at a time, when 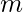 particular things never come together –
particular things never come together –
Permutations = n! - (n-m+1)! × m!
Below is the implementation of above approach –
C++
#include<bits/stdc++.h>
using namespace std;
int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i ;
return (fact);
}
int result(int n, int m)
{
return(factorial(n) -
factorial(n - m + 1) *
factorial(m));
}
int main()
{
cout(result(5, 3));
}
|
Java
class GFG
{
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i ;
return (fact);
}
static int result(int n, int m)
{
return(factorial(n) -
factorial(n - m + 1) *
factorial(m));
}
public static void main(String args[])
{
System.out.println(result(5, 3));
}
}
|
Python3
def factorial(n):
fact = 1;
for i in range(2, n + 1):
fact = fact * i
return (fact)
def result(n, m):
return(factorial(n) - factorial(n - m + 1) * factorial(m))
print(result(5, 3))
|
C#
using System;
class GFG
{
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i ;
return (fact);
}
static int result(int n, int m)
{
return(factorial(n) -
factorial(n - m + 1) *
factorial(m));
}
public static void Main()
{
Console.WriteLine(result(5, 3));
}
}
|
Javascript
<script>
function factorial(n)
{
let fact = 1;
for (let i = 2; i <= n; i++)
fact = fact * i ;
return (fact);
}
function result(n, m)
{
return(factorial(n) -
factorial(n - m + 1) *
factorial(m));
}
document.write(result(5, 3));
</script>
|
Output :
84
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...