Paths with maximum number of ‘a’ from (1, 1) to (X, Y) vertically or horizontally
Given a N X N matrix consisting of characters. Also given are Q queries, where each query contains a co-ordinate (X, Y). For every query, find all paths from (1, 1) to (X, Y) by either moving vertically or horizontally and take the path which has the maximum number of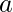 
in it. The task is to print the number of non-‘a’-characters along that path.
Examples:
Input: mat[][] = {{'a', 'b', 'a'},
{'a', 'c', 'd'},
{'b', 'a', 'b'}}
Queries:
X = 1, Y = 3
X = 3, Y = 3
Output:
1st query: 1
2nd query: 2
Query-1: There is only one path from (1, 1) to (1, 3)
i.e., "aba" and the number of characters
which are not 'a' is 1.
Query-2: The path which has the maximum number of 'a'
in it is "aabab", hence non 'a'
characters are 2.
The problem is a variant of Min-Cost path Dp problem. We need to pre-compute the DP[][] array and then the answer will be DP[X][Y], hence every query can be answered in O(1). If the index position (1, 1) character is not ‘a’, then increase the dp[1][1] value by 1. Then simply iterate for rows and columns, and do a min-cost DP considering ‘a’ as 1 and non-‘a’ character as 0. Since the DP[][] array stores the min-cost path from (1, 1) to any index (i, j), hence the query can be answered in O(1).
Below is the implementation of the above approach:
C++
// C++ program to find paths with maximum number // of 'a' from (1, 1) to (X, Y) vertically // or horizontally #include <bits/stdc++.h> using namespace std; const int n = 3; int dp[n][n]; // Function to answer queries void answerQueries(pair<int, int> queries[], int q) { // Iterate till query for (int i = 0; i < q; i++) { // Decrease to get 0-based indexing int x = queries[i].first; x--; int y = queries[i].second; y--; // Print answer cout << dp[x][y] << endl; } } // Function that pre-computes the dp array void pre_compute(char a[][n]) { // Check fo the first character if (a[0][0] == 'a') dp[0][0] = 0; else dp[0][0] = 1; // Iterate in row and columns for (int row = 0; row < n; row++) { for (int col = 0; col < n; col++) { // If not first row or not first coloumn if (row != 0 || col != 0) dp[row][col] = INT_MAX; // Not first row if (row != 0) { dp[row][col] = min(dp[row][col], dp[row - 1][col]); } // Not first coloumn if (col != 0) { dp[row][col] = min(dp[row][col], dp[row][col - 1]); } // If it is not 'a' then increase by 1 if (a[row][col] != 'a' && (row != 0 || col != 0)) dp[row][col] += 1; } } } // Driver code int main() { // character N X N array char a[][3] = { { 'a', 'b', 'a' }, { 'a', 'c', 'd' }, { 'b', 'a', 'b' } }; // queries pair<int, int> queries[] = { { 1, 3 }, { 3, 3 } }; // number of queries int q = 2; // function call to pre-compute pre_compute(a); // function call to answer every query answerQueries(queries, q); } |
Java
// Java program to find paths with maximum number // of 'a' from (1, 1) to (X, Y) vertically // or horizontally class GFG { static class pair { int first, second; public pair(int first, int second) { this.first = first; this.second = second; } } static int n = 3; static int [][]dp = new int[n][n]; // Function to answer queries static void answerQueries(pair queries[], int q) { // Iterate till query for (int i = 0; i < q; i++) { // Decrease to get 0-based indexing int x = queries[i].first; x--; int y = queries[i].second; y--; // Print answer System.out.println(dp[x][y]); } } // Function that pre-computes the dp array static void pre_compute(char a[][]) { // Check fo the first character if (a[0][0] == 'a') dp[0][0] = 0; else dp[0][0] = 1; // Iterate in row and columns for (int row = 0; row < n; row++) { for (int col = 0; col < n; col++) { // If not first row or not first coloumn if (row != 0 || col != 0) dp[row][col] = Integer.MAX_VALUE; // Not first row if (row != 0) { dp[row][col] = Math.min(dp[row][col], dp[row - 1][col]); } // Not first coloumn if (col != 0) { dp[row][col] = Math.min(dp[row][col], dp[row][col - 1]); } // If it is not 'a' then increase by 1 if (a[row][col] != 'a' && (row != 0 || col != 0)) dp[row][col] += 1; } } } // Driver code public static void main(String[] args) { // character N X N array char a[][] = {{ 'a', 'b', 'a' }, { 'a', 'c', 'd' }, { 'b', 'a', 'b' }}; // queries pair queries[] = { new pair( 1, 3 ), new pair(3, 3 ) }; // number of queries int q = 2; // function call to pre-compute pre_compute(a); // function call to answer every query answerQueries(queries, q); } } // This code is contributed by 29AjayKumar |
C#
// C# program to find paths with maximum number // of 'a' from (1, 1) to (X, Y) vertically // or horizontally using System; class GFG { class pair { public int first, second; public pair(int first, int second) { this.first = first; this.second = second; } } static int n = 3; static int [,]dp = new int[n, n]; // Function to answer queries static void answerQueries(pair []queries, int q) { // Iterate till query for (int i = 0; i < q; i++) { // Decrease to get 0-based indexing int x = queries[i].first; x--; int y = queries[i].second; y--; // Print answer Console.WriteLine(dp[x, y]); } } // Function that pre-computes the dp array static void pre_compute(char [,]a) { // Check fo the first character if (a[0, 0] == 'a') dp[0, 0] = 0; else dp[0, 0] = 1; // Iterate in row and columns for (int row = 0; row < n; row++) { for (int col = 0; col < n; col++) { // If not first row or not first coloumn if (row != 0 || col != 0) dp[row, col] = int.MaxValue; // Not first row if (row != 0) { dp[row, col] = Math.Min(dp[row, col], dp[row - 1, col]); } // Not first coloumn if (col != 0) { dp[row, col] = Math.Min(dp[row, col], dp[row, col - 1]); } // If it is not 'a' then increase by 1 if (a[row, col] != 'a' && (row != 0 || col != 0)) dp[row, col] += 1; } } } // Driver code public static void Main(String[] args) { // character N X N array char [,]a = {{ 'a', 'b', 'a' }, { 'a', 'c', 'd' }, { 'b', 'a', 'b' }}; // queries pair []queries = { new pair(1, 3), new pair(3, 3) }; // number of queries int q = 2; // function call to pre-compute pre_compute(a); // function call to answer every query answerQueries(queries, q); } } // This code is contributed by PrinciRaj1992 |
Output:
1 2
Time Complexity: O(N2) for pre-computation and O(1) for each query.
Auxiliary Space: O(N2)
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.
