Number of ways to reach (M, N) in a matrix starting from the origin without visiting (X, Y)
Last Updated :
06 Sep, 2022
Given four positive integers M, N, X, and Y, the task is to count all the possible ways to reach from the top left(i.e., (0, 0)) to the bottom right (M, N) of a matrix of size (M+1)x(N+1) without visiting the cell (X, Y). It is given that from each cell (i, j) you can either move only to right (i, j + 1) or down (i + 1, j).
Examples:
Input: M = 2, N = 2, X = 1, Y = 1
Output: 2
Explanation:
There are only 2 ways to reach (2, 2) without visiting (1, 1) and the two paths are:
(0, 0) -> (0, 1) -> (0, 2) -> (1, 2) -> (2, 2)
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) -> (2, 2)
Input: M = 5, N = 4, X = 3, Y = 2
Output: 66
Explanation:
There are 66 ways to reach (5, 4) without visiting (3, 2).
Approach:
To solve the problem mentioned above the idea is to subtract the number of ways to reach from (0, 0) to (X, Y) which was followed by reaching (M, N) from (X, Y) by visiting (X, Y) from the total number of ways reaching (M, N) from (0, 0).
Therefore,
- The number of ways to reach from (M, N) from the origin (0, 0) is given by:
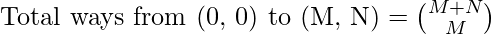
- The number of ways to reach (M, N) only by visiting (X, Y) is reaching (X, Y) from (0, 0) which was followed by reaching (M, N) from (X, Y) is given by:
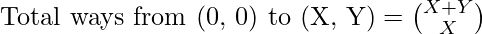
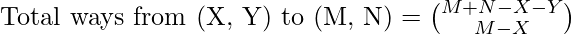
Therefore,
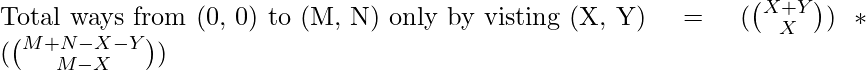
- Hence, the equation for the total number of ways are:
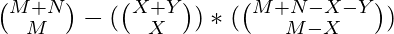
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int fact(int n);
int nCr(int n, int r)
{
return fact(n)
/ (fact(r) * fact(n - r));
}
int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
int countWays(int m, int n, int x, int y)
{
return nCr(m + n, m)
- nCr(x + y, x) * nCr(m + n
- x - y,
m - x);
}
int main()
{
int m = 5;
int n = 4;
int x = 3;
int y = 2;
cout << countWays(m, n, x, y);
return 0;
}
|
Java
import java.util.*;
class GFG{
public static int nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
public static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
public static int countWays(int m, int n,
int x, int y)
{
return nCr(m + n, m) -
nCr(x + y, x) *
nCr(m + n - x - y, m - x);
}
public static void main(String[] args)
{
int m = 5;
int n = 4;
int x = 3;
int y = 2;
System.out.println(countWays(m, n, x, y));
}
}
|
Python3
def nCr(n, r):
return (fact(n) // (fact(r) *
fact(n - r)))
def fact(n):
res = 1
for i in range(2, n + 1):
res = res * i
return res
def countWays(m, n, x, y):
return (nCr(m + n, m) - nCr(x + y, x) *
nCr(m + n - x - y, m - x))
m = 5
n = 4
x = 3
y = 2
print(countWays(m, n, x, y))
|
C#
using System;
class GFG{
public static int nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
public static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
public static int countWays(int m, int n,
int x, int y)
{
return nCr(m + n, m) -
nCr(x + y, x) *
nCr(m + n - x - y, m - x);
}
public static void Main(String[] args)
{
int m = 5;
int n = 4;
int x = 3;
int y = 2;
Console.WriteLine(countWays(m, n, x, y));
}
}
|
Javascript
<script>
function nCr(n, r)
{
return fact(n) / (fact(r) * fact(n - r));
}
function fact(n)
{
let res = 1;
for(let i = 2; i <= n; i++)
res = res * i;
return res;
}
function countWays(m, n, x, y)
{
return nCr(m + n, m) -
nCr(x + y, x) *
nCr(m + n - x - y, m - x);
}
let m = 5;
let n = 4;
let x = 3;
let y = 2;
document.write(countWays(m, n, x, y));
</script>
|
Time Complexity: O(M + N), where M, N represents the size of the matrix.
Auxiliary Space: O(1), as constant space is required.
Share your thoughts in the comments
Please Login to comment...