Pareto Optimality and its application in Game Theory
Last Updated :
07 Feb, 2020
Prerequisites: Game Theory
When the strategies from game theory are discussed, they are often mentioned from a player’s perspective. However, when the strategies are formed from an observer’s angle whose main motive is to wish for the best outcome for every player; that is, when strategies are formed from a socially balanced viewpoint, then the outcome is known as a Pareto Optimal outcome.
An outcome is said to be Pareto optimal if it cannot be Pareto dominated by any other outcome. To be specific on choosing a Pareto outcome, it is evident that no other outcome can prove to be better than this outcome for all the players. In addition to this, one player strictly chooses the Pareto optimal outcome over any other outcome.
For example, consider two outcomes with payoffs to the two players as (5, 8) and (5, 6). Here, it is evident that choosing any of the outcomes would mean no difference to player one as he/she would receive a payoff of 5 either way. However, choosing the first outcome would change things a tad bit in the favour of player two as he/she would receive an 8 instead of a 6. Therefore, choosing the first outcome means that both players get the best payoff they can and that is why this is the Pareto optimal outcome in this case.
Let us consider a few popular two-player games and analyse the Pareto optimal outcome in each of these:
-
The Coordination game: The scenario in this game is comparable to two people walking on pavement from opposite directions. If both choose to stick to their respective right or left, it will prove to be advantageous to both. However, if either of them deviates from this choice, they are prone to collision. The payoff matrix for this game is as follows:

From the matrix above, it is clear that the outcomes (1, 1) are Pareto optimal for this game.
- The Battle of the Sexes: This can be thought off as a situation between a husband and a wife. The husband puts forward an idea of going to a boxing match, and the wife for obvious reasons prefers shopping over boxing. They have different interests, but most importantly both want to spend the day together. This means that the wife would go to the boxing match with her husband, where she would end up getting a payoff of one along with the husband enjoying his payoff of two, rather than going shopping alone, where both would just receive a zero payoff. The payoff matrix for this game looks something like this:
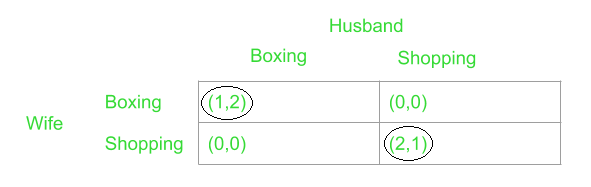
Therefore, we can observe that (2, 1) and (1, 2) are the Pareto optimal outcomes in this case.
- The Matching pennies game: The objective of the game is different for the two players. Both players are given coins with two faces a head and a tail. Player one must try and match his penny with that of player two and player two must make sure his/her penny doesn’t match player one. So, in cases where the pennies match, player one gets some positive payoff along with player two getting an equal negative payoff. Conversely, on a mismatch player two is rewarded a positive payoff and player one a negative. The given payoff matrix better demonstrates this:
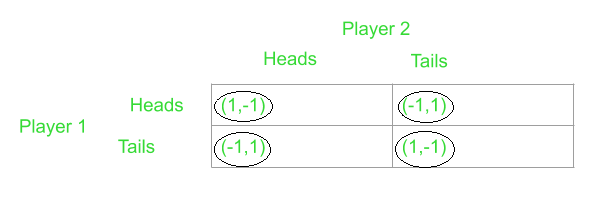
In this game, if player one chooses to play heads, player two would obviously respond with tails. Again if player two chose tails, player one would be interested to play tails in order to win and these choices would repeat themselves in a cyclic manner. Therefore, it is evident that each player’s decision is directly influenced by the other’s and there is no dominant strategy any player would choose to win. As a result, all the outcomes in the payoff matrix are essentially Pareto optimal which is quite common in case of zero-sum games.
- The Prisoner’s dilemma: Let us consider two prisoners who are convicted for a certain crime. Due to some lack of evidence, the prisoners are sentenced to one year of imprisonment only. Now both the prisoners are spoken to in confidence and are offered to be set free if they betray the other. However, the person who gets betrayed now receives ten-year imprisonment which is a larger negative payoff. Also, if both the prisoners betray each other, then both are sentenced to five-year imprisonment each.
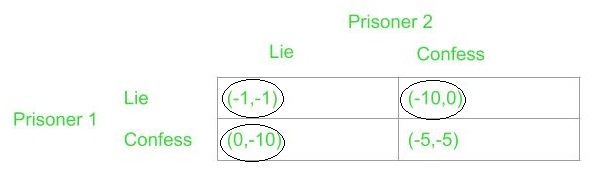
It is quite intriguing that the outcomes (-1, -1), (0, -10) and (-10, 0) are all Pareto optimal for this game. The outcome (-5, -5) is not Pareto optimal as it is Pareto dominated by the outcome (-1, -1). Another interesting observation to make is that (-5, -5) which is the only Non-Pareto optimal outcome in the game is also the dominant strategy every player is expected to play, making it the Nash equilibrium. This is why the prisoner’s dilemma is such a dilemma!
Share your thoughts in the comments
Please Login to comment...