The term broadcasting refers to the ability of NumPy to treat arrays with different dimensions during arithmetic operations. This process involves certain rules that allow the smaller array to be ‘broadcast’ across the larger one, ensuring that they have compatible shapes for these operations.
Broadcasting is not limited to two arrays; it can be applied over multiple arrays as well.
In this article, we will learn about broadcast over multiple arrays in the NumPy extension in Python.
What is NumPy Array Broadcasting?
Broadcasting provides a means of vectorizing array operations, therefore eliminating the need for Python loops. This is because NumPy is implemented in C Programming, which is a very efficient language.
It does this without making needless copies of data which leads to efficient algorithm implementations. But broadcasting over multiple arrays in NumPy extension can raise cases where broadcasting is a bad idea because it leads to inefficient use of memory that slows down the computation.
The resulting array returned after broadcasting will have the same number of dimensions as the array with the greatest number of dimensions.
Array Element-wise Multiplication
In this example, the code multiplies element-wise arrays ‘a’ and ‘b’ with compatible dimensions, storing the result in array ‘c’ and printing it.
Python3
import numpy as np
a = np.array([5, 7, 3, 1])
b = np.array([90, 50, 0, 30])
c = a * b
print(c)
|
Output:
[450, 350, 0, 30]
NumPy Broadcasting Arrays in Python
Let’s assume that we have a large data set, each data is a list of parameters. In Numpy, we have a 2-D array, where each row is data and the number of rows is the size of the data set. Suppose we want to apply some sort of scaling to all these data every parameter gets its scaling factor or say every parameter is multiplied by some factor.
Just to have a clear understanding, let’s count calories in foods using a macro-nutrient breakdown. Roughly put, the caloric parts of food are made of fats (9 calories per gram), protein (4 CPG), and carbs (4 CPG).
So if we list some foods (our data), and for each food list its macro-nutrient breakdown (parameters), we can then multiply each nutrient by its caloric value (apply scaling) to compute the caloric breakdown of every food item.
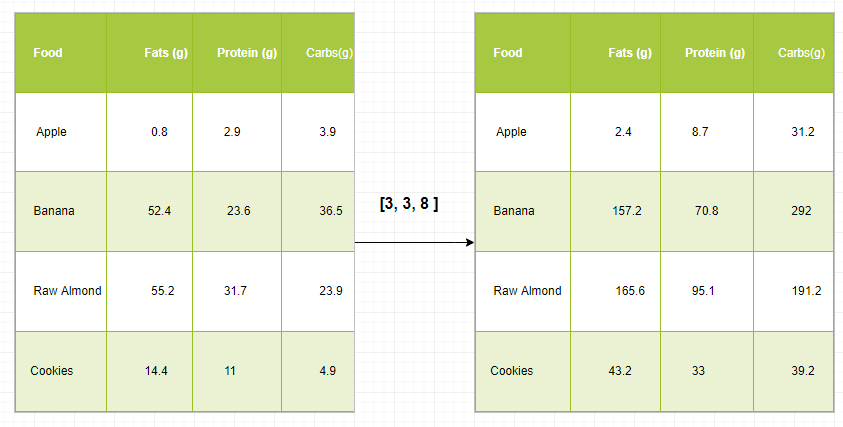
With this transformation, we can now compute all kinds of useful information. For example, what is the total number of calories present in some food, or given a breakdown of my dinner know how many calories did I get from protein and so on?
Example: Broadcasting Array- Element Wise Multiplication
In this example, the code initializes a 2D array ‘macros’ representing nutritional values.
It then creates a new array ‘result’ filled with zeros, having the same shape as ‘macros.’
Another array ‘cal_per_macro’ is defined. Finally, it multiplies each row of ‘macros’ by ‘cal_per_macro,’ storing the results in ‘result,’.
Python3
macros = array([
[0.8, 2.9, 3.9],
[52.4, 23.6, 36.5],
[55.2, 31.7, 23.9],
[14.4, 11, 4.9]
])
result = zeros_like(macros)
cal_per_macro = array([3, 3, 8])
for i in range(macros.shape[0]):
result[i, :] = macros[i, :] * cal_per_macro
result
|
Output:
array([[ 2.4, 8.7, 31.2 ],
[ 157.2, 70.8, 292 ],
[ 165.6, 95.1, 191.2],
[ 43.2, 33, 39.2]])
Array Broadcasting Algorithm
The NumPy array broadcasting algorithm determines how NumPy will treat arrays with different shapes during arithmetic operations.
Input: Array ‘A’ with ‘m’ dimensions and array ‘B’ with ‘n’ dimensions
p = max(m, n)
if m < p:
left-pad A's shape with 1s until it also has p dimensions
else if n < p:
left-pad B's shape with 1s until it also has p dimensions
result_dims = new list with p elements
for i in p-1 ... 0:
A_dim_i = A.shape[i]
B_dim_i = B.shape[i]
if A_dim_i != 1 and B_dim_i != 1 and A_dim_i != B_dim_i:
raise ValueError("could not broadcast")
else:
# Pick the Array which is having maximum Dimension
result_dims[i] = max(A_dim_i, B_dim_i)
Rules for Broadcasting
Broadcasting arrays is possible if the following rules are met:
- If the arrays don’t have the same rank then prepend the shape of the lower rank array with 1s until both shapes have the same length.
- The two arrays are compatible in a dimension if they have the same size in the dimension or if one of the arrays has size 1 in that dimension.
- The arrays can be broadcast together if they are compatible with all dimensions.
- After broadcasting, each array behaves as if it had a shape equal to the element-wise maximum of shapes of the two input arrays.
- In any dimension where one array had size 1 and the other array had size greater than 1, the first array behaves as if it were copied along that dimension.
What makes an array Broadcastable?
An array can be considered broadcastable if it satisfies the following rules:
- The arrays have the same shapes
- The arrays have the same number of dimensions and the length of each dimension is either of common length or 1.
- If an array has a different number of dimensions then the array with fewer dimensions can have its shape prepended.
Array Broadcasting Examples
Below are some examples of NumPy array broadcasting in Python:
Array Broadcasting of Single-Dimensional Array
In this example, the code uses NumPy to create a 1×3 array ‘a’ with elements [17, 11, 19]. It then defines a scalar ‘b’ with a value of 3. Broadcasting is employed when adding ‘a’ and ‘b’ (a + b), performing element-wise addition, resulting in a new array ‘c’ with elements [20, 14, 22].
Python3
import numpy as np
a = np.array([17, 11, 19])
print(a)
b = 3
print(b)
c = a + b
print(c)
|
Output:
[17 11 19]
3
[20 14 22]
Array Broadcasting of Two-Dimensional Array
In this example, we are creating a 2×3 NumPy array ‘A’ and printing it. We then define a scalar ‘b’ with the value 4 and print it. Finally, we add ‘b’ to each element of ‘A’ to create a new array ‘C’ and print it.
Example
Python3
import numpy as np
A = np.array([[11, 22, 33], [10, 20, 30]])
print(A)
b = 4
print(b)
C = A + b
print(C)
|
Output:
[[11 22 33]
[10 20 30]]
4
[[15 26 37]
[14 24 34]]
NumPy Broadcasting Operations
In this example, the code showcases NumPy broadcasting operations:
- Computing the outer product of vectors
- Broadcasting a vector to a matrix,
- Broadcasting a vector to the transposed matrix,
- Reshaping and broadcasting a vector to a matrix, and
- Performing scalar multiplication on a matrix.
Python3
import numpy as np
v = np.array([1, 2, 3])
w = np.array([4, 5])
print(np.reshape(v, (3, 1)) * w)
x = np.array([[1, 2, 3], [4, 5, 6]])
print(x + v)
print((x.T + w).T)
print(x + np.reshape(w, (2, 1)))
print(x * 2)
|
Output:
[[ 4 5]
[ 8 10]
[12 15]]
[[2 4 6]
[5 7 9]]
[[ 5 6 7]
[ 9 10 11]]
[[ 5 6 7]
[ 9 10 11]]
[[ 2 4 6]
[ 8 10 12]]
Broadcasting for Plotting a Two-Dimensional Function
Broadcasting is also frequently used in displaying images based on two-dimensional functions. If we want to define a function z=f(x, y).
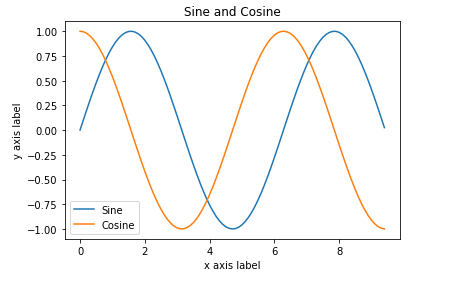
In this example, we are utilizing NumPy and Matplotlib to generate and plot the sine and cosine curves. It first creates arrays for x coordinates ranging from 0 to 3π with a step of 0.1. Then, it computes the corresponding y values for sine and cosine functions.
Python3
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
plt.plot(x, y_sin)
plt.plot(x, y_cos)
plt.xlabel('x axis label')
plt.ylabel('y axis label')
plt.title('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])
plt.show()
|
Output:
Conclusion
Broadcasting is a very reliable feature offered by the NumPy library in Python. It lets you perform arithmetic operations on arrays of different shapes.
In this tutorial, we have explained all about NumPy array broadcasting covering its meaning, rules, and examples. This guide has explained all the concepts easily with sample Python programs to give a practical approach to NumPy array broadcasting.
Share your thoughts in the comments
Please Login to comment...