Vectorization in Python

We know that most of the application has to deal with a large number of datasets. Hence, a non-computationally-optimal function can become a huge bottleneck in your algorithm and can take result in a model that takes ages to run. To make sure that the code is computationally efficient, we will use vectorization.

Time complexity in the execution of any algorithm is very crucial deciding whether an application is reliable or not. To run a large algorithm in as much as optimal time possible is very important when it comes to real-time application of output. To do so, Python has some standard mathematical functions for fast operations on entire arrays of data without having to write loops. One of such library which contains such function is numpy. Let’s see how can we use this standard function in case of vectorization.

What is Vectorization ?
Vectorization is used to speed up the Python code without using loop. Using such a function can help in minimizing the running time of code efficiently. Various operations are being performed over vector such as dot product of vectors which is also known as scalar product as it produces single output, outer products which results in square matrix of dimension equal to length X length of the vectors, Element wise multiplication which products the element of same indexes and dimension of the matrix remain unchanged.

We will see how the classic methods are more time consuming than using some standard function by calculating their processing time.

outer(a, b): Compute the outer product of two vectors.
multiply(a, b): Matrix product of two arrays.
dot(a, b): Dot product of two arrays.
zeros((n, m)): Return a matrix of given shape and type, filled with zeros.
process_time(): Return the value (in fractional seconds) of the sum of the system and user CPU time of the current process. It does not include time elapsed during sleep.

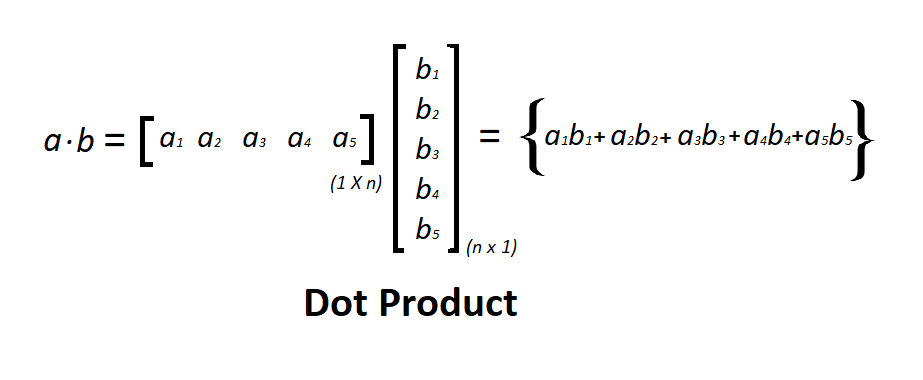
Dot Product:
Dot product is an algebraic operation in which two equal length vectors are being multiplied such that it produces a single number. Dot Product often called as inner product. This product results in a scalar number. Let’s consider two matrix a and b of same length, the dot product is done by taking the transpose of first matrix and then mathematical matrix multiplication of a’(transpose of a) and b is followed as shown in the figure below.

Pictorial representation of dot product –

Below is the Python code:

# Dot product
import time
import numpy
import array

# 8 bytes size int
a = array.array('q')
for i in range(100000):
    a.append(i);

b = array.array('q')
for i in range(100000, 200000):
    b.append(i)

# classic dot product of vectors implementation
tic = time.process_time()
dot = 0.0;

for i in range(len(a)):
      dot += a[i] * b[i]

toc = time.process_time()

print("dot_product = "+ str(dot));
print("Computation time = " + str(1000*(toc - tic )) + "ms")


n_tic = time.process_time()
n_dot_product = numpy.dot(a, b)
n_toc = time.process_time()

print("\nn_dot_product = "+str(n_dot_product))
print("Computation time = "+str(1000*(n_toc - n_tic ))+"ms")

Output:

dot_product = 833323333350000.0
Computation time = 35.59449199999999ms

n_dot_product = 833323333350000
Computation time = 0.1559900000000225ms

Outer Product:
The tensor product of two coordinate vectors is termed as Outer product. Let’s consider two vectors a and b with dimension n x 1 and m x 1 then the outer product of the vector results in a rectangular matrix of n x m. If two vectors have same dimension then the resultant matrix will be a square matrix as shown in the figure.

Pictorial representation of outer product –

Below is the Python code:

# Outer product
import time
import numpy
import array

a = array.array('i')
for i in range(200):
    a.append(i);

b = array.array('i')
for i in range(200, 400):
    b.append(i)

# classic outer product of vectors implementation
tic = time.process_time()
outer_product = numpy.zeros((200, 200))

for i in range(len(a)):
   for j in range(len(b)):
      outer_product[i][j]= a[i]*b[j]

toc = time.process_time()

print("outer_product = "+ str(outer_product));
print("Computation time = "+str(1000*(toc - tic ))+"ms")

n_tic = time.process_time()
outer_product = numpy.outer(a, b)
n_toc = time.process_time()

print("outer_product = "+str(outer_product));
print("\nComputation time = "+str(1000*(n_toc - n_tic ))+"ms")

Output:

outer_product = [[     0.      0.      0. ...,      0.      0.      0.]
 [   200.    201.    202. ...,    397.    398.    399.]
 [   400.    402.    404. ...,    794.    796.    798.]
 ..., 
 [ 39400.  39597.  39794. ...,  78209.  78406.  78603.]
 [ 39600.  39798.  39996. ...,  78606.  78804.  79002.]
 [ 39800.  39999.  40198. ...,  79003.  79202.  79401.]]

Computation time = 39.821617ms

outer_product = [[    0     0     0 ...,     0     0     0]
 [  200   201   202 ...,   397   398   399]
 [  400   402   404 ...,   794   796   798]
 ..., 
 [39400 39597 39794 ..., 78209 78406 78603]
 [39600 39798 39996 ..., 78606 78804 79002]
 [39800 39999 40198 ..., 79003 79202 79401]]

Computation time = 0.2809480000000031ms

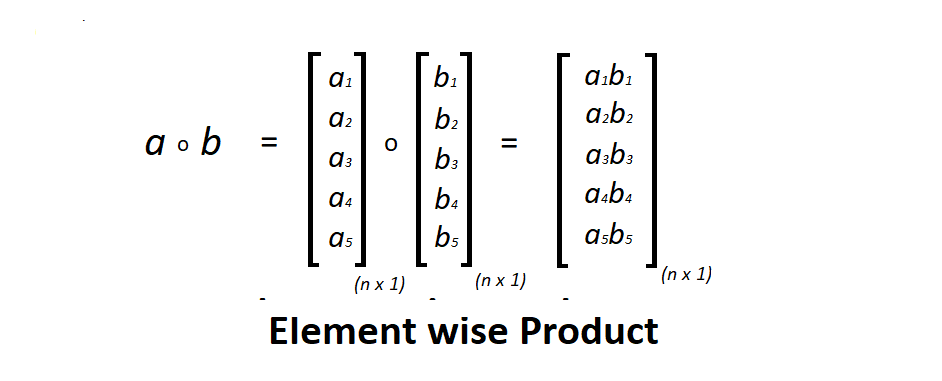
Element wise Product:
Element-wise multiplication of two matrices is the algebraic operation in which each element of first matrix is multiplied by its corresponding element in the later matrix. Dimension of the matrices should be same.
Consider two matrices a and b, index of an element in a is i and j then a(i, j) is multiplied with b(i, j) respectively as shown in the figure below.

Pictorial representation of Element wise product –

Below is the Python code:

# Element-wise multiplication
import time
import numpy
import array

a = array.array('i')
for i in range(50000):
    a.append(i);

b = array.array('i')
for i in range(50000, 100000):
    b.append(i)

# classic element wise product of vectors implementation
vector = numpy.zeros((50000))

tic = time.process_time()

for i in range(len(a)):
      vector[i]= a[i]*b[i]

toc = time.process_time()

print("Element wise Product = "+ str(vector));
print("\nComputation time = "+str(1000*(toc - tic ))+"ms")


n_tic = time.process_time()
vector = numpy.multiply(a, b)
n_toc = time.process_time()

print("Element wise Product = "+str(vector));
print("\nComputation time = "+str(1000*(n_toc - n_tic ))+"ms")

Output:

Element wise Product = [  0.00000000e+00   5.00010000e+04   1.00004000e+05 ...,   4.99955001e+09
   4.99970000e+09   4.99985000e+09]

Computation time = 23.516678000000013ms

Element wise Product = [        0     50001    100004 ..., 704582713 704732708 704882705]
Computation time = 0.2250640000000248ms