Number of ways to place two queens on a N*N chess-board

Given an integer N denoting a N * N chess-board, the task is to count the number of ways to place two queens on the board such that, they do not attack each other.

Examples:

Input: N = 9 
Output: 2184 
Explanation:
There are 2184 ways to place two queens on 9 * 9 chess-board.

Input: N = 3 
Output: 8 
Explanation:
There are 8 ways to place two queens on 3 * 3 chess-board.

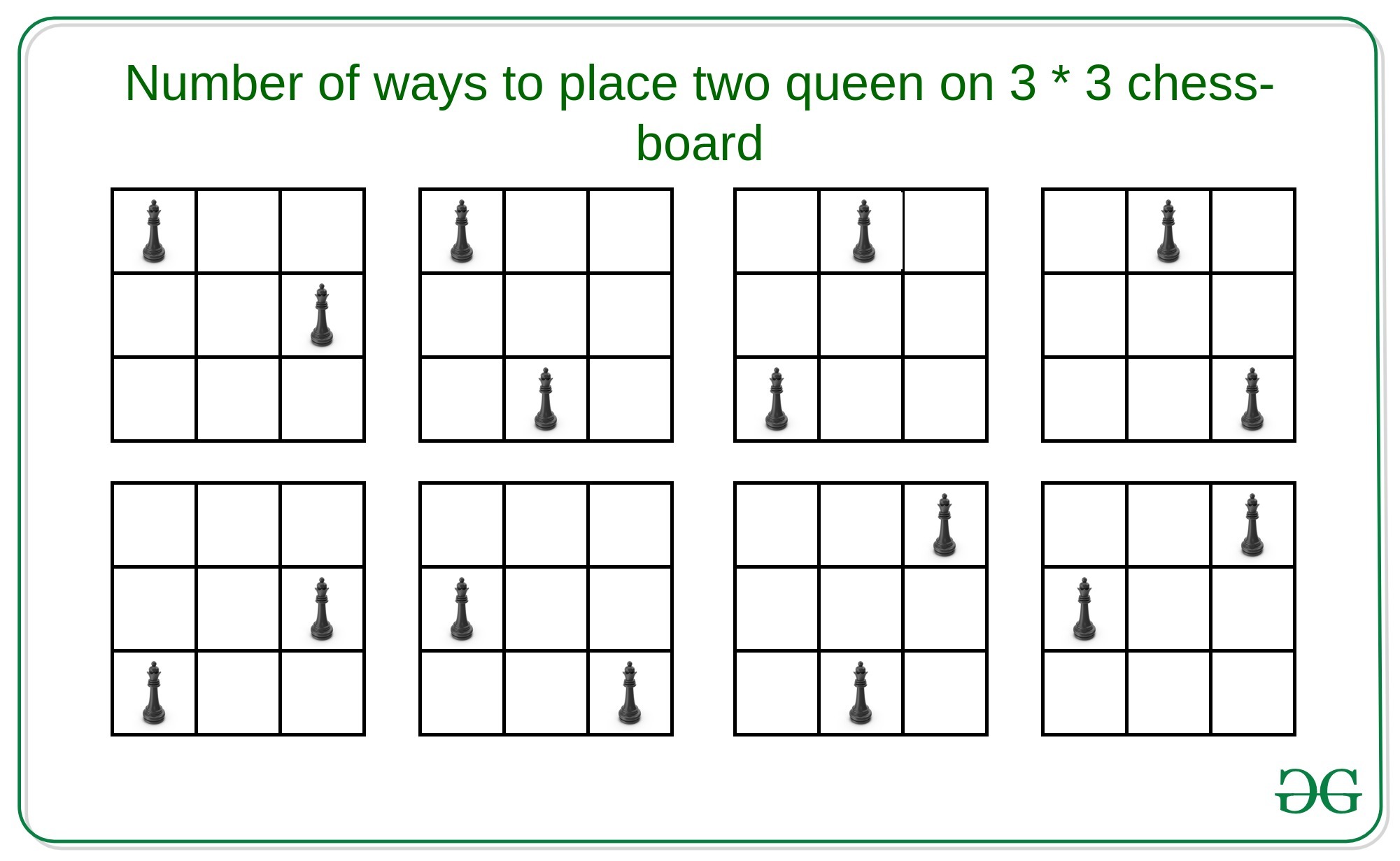
Naive Approach: A simple solution will be to choose two every possible position for the two queens on the N * N matrix and check that they are not in horizontal, vertical, positive diagonal or negative diagonal. If yes then increment the count by 1. 
Time Complexity: O(N⁴)

Efficient Approach: The idea is to use combinations to compute the possible positions of the queens such that they do not attack each other. A useful observation is that it is quite easy to calculate the number of positions that a single queen attacks. That is –

Number of positions a queen attack = (N - 1) + (N - 1) + (D - 1)

Here, 
// First N-1 denotes positions in horizontal direction
// Second N-1 denotes positions in vertical direction
// D = Number of positions in 
    positive and negative diagonal

If we do not place the queen on the last row and the last column then the answer will simply be the number of positions to place in a chessboard of  whereas if we place in the last column and last row then possible positions for queens will be 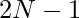 and attacking at  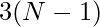positions. Therefore, the possible positions for the other queen for each position of the queen will be 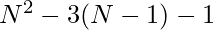. Finally, there are 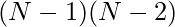combinations where both queens are on the last row and last column. Therefore, the recurrence relation will be:

// By Induction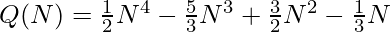

Below is the implementation of the above approach:

C++

// C++ implementation to find the
// number of ways to place two
// queens on the N * N chess board

#include <bits/stdc++.h>

#define ll long long
using namespace std;

// Function to find number of valid
// positions for two queens in the
// N * N chess board
ll possiblePositions(ll n)
{
    ll term1 = pow(n, 4);
    ll term2 = pow(n, 3);
    ll term3 = pow(n, 2);
    ll term4 = n / 3;
    ll ans = (ceil)(term1) / 2 -
             (ceil)(5 * term2) / 3 +
             (ceil)(3 * term3) / 2 - term4;
    return ans;
}

// Driver Code
int main()
{
    ll n;
    n = 3;

    // Function Call
    ll ans = possiblePositions(n);
    cout << ans << endl;
    return 0;
}

Java

// Java implementation to find the
// number of ways to place two
// queens on the N * N chess board
class GFG{

// Function to find number of valid
// positions for two queens in the
// N * N chess board
static double possiblePositions(double n)
{
    double term1 = Math.pow(n, 4);
    double term2 = Math.pow(n, 3);
    double term3 = Math.pow(n, 2);
    double term4 = n / 3;
    double ans = (Math.ceil(term1 / 2)) -
                 (Math.ceil(5 * term2) / 3) +
                 (Math.ceil(3 * term3) / 2) - term4;

    return (long)ans;
}

// Driver Code
public static void main(String[] args)
{
    double n;
    n = 3;

    // Function Call
    double ans = possiblePositions(n);
    System.out.print(ans + "\n");
}
}

// This code is contributed by sapnasingh4991

Python3

# Python3 implementation to find the
# number of ways to place two
# queens on the N * N chess board
import math

# Function to find number of valid
# positions for two queens in the
# N * N chess board
def possiblePositions(n):

    term1 = pow(n, 4);
    term2 = pow(n, 3);
    term3 = pow(n, 2);
    term4 = n / 3;

    ans = ((math.ceil(term1)) / 2 -
           (math.ceil(5 * term2)) / 3 +
           (math.ceil(3 * term3)) / 2 - term4);

    return ans;

# Driver code
if __name__ == '__main__':

    n = 3

    # Function call
    ans = possiblePositions(n)

    print(int(ans))

# This code is contributed by jana_sayantan

C#

// C# implementation to find the
// number of ways to place two
// queens on the N * N chess board
using System;

class GFG{

// Function to find number of valid
// positions for two queens in the
// N * N chess board
static double possiblePositions(double n)
{
    double term1 = Math.Pow(n, 4);
    double term2 = Math.Pow(n, 3);
    double term3 = Math.Pow(n, 2);
    double term4 = n / 3;
    double ans = (Math.Ceiling(term1 / 2)) -
                 (Math.Ceiling(5 * term2) / 3) +
                 (Math.Ceiling(3 * term3) / 2) - term4;

    return (long)ans;
}

// Driver Code
public static void Main(String[] args)
{
    double n;
    n = 3;

    // Function Call
    double ans = possiblePositions(n);
    Console.Write(ans + "\n");
}
}

// This code is contributed by Amit Katiyar

Javascript

<script>

// Javascript implementation to find the
// number of ways to place two
// queens on the N * N chess board

// Function to find number of valid
// positions for two queens in the
// N * N chess board
function possiblePositions(n)
{
    let term1 = Math.pow(n, 4);
    let term2 = Math.pow(n, 3);
    let term3 = Math.pow(n, 2);
    let term4 = n / 3;
    let ans = (Math.ceil(term1 / 2)) -
                 (Math.ceil(5 * term2) / 3) +
                 (Math.ceil(3 * term3) / 2) - term4;

    return ans;
}

    // Driver Code
    let n;
    n = 3;

    // Function Call
    let ans = possiblePositions(n);
    document.write(Math.floor(ans));

// This code is contributed by souravghosh0416.
</script>

Output:

8

Time Complexity: O(1)
Auxiliary Space: O(1)