Number of edges in mirror image of Complete binary tree
Last Updated :
08 Mar, 2023
Given a complete binary tree of depth H. If the mirror image from the left and the right side of this tree is taken then:
Right Mirrored Image: Rightmost node of the every level is connected to mirrored corresponding node.
Left Mirrored Image: Left most node of the every level is connected to mirrored corresponding node.
The task is to find the number of edges after taking both the mirror images in the final tree.

Examples:
Input: H = 1
Output: 10
2 edges in the original tree will get mirrored in the mirror images (left and right) i.e. 6 edges in total.
And the edges connecting the mirror images with the original tree as shown in the image above.
Input: H = 2
Output: 24
(6 * 3) + 3 + 3 = 24
Approach: Maintain the leftmost, rightmost nodes after each mirror image. Number of edges will change after each operation of mirror image. Initially,

After right mirrored image: 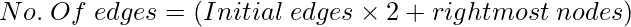
After left mirrored image: 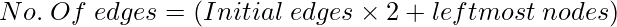
In complete modified tree: 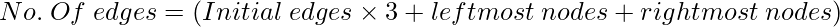
Algorithm:
Step 1: Start
Step 2: Create a function named “countEdges” of int return type and takes an integer value as a parameter.
Step 3: Now, in the “countEdges” function let’s declare three variables to store integer values
named “edges”, “right”, and “left”.
Step 4: Using the formula 2*(pow()2, H)-1), determine the total number of edges in the entire binary tree of height ‘H’.
Step 5: Use formula 2 to determine how many nodes are in the final level of the entire binary tree (H).
Step 6: Set ‘left’ and ‘right’ variables to H+1.
Step 7: Now, let’s calculate the total number of edges in the modified tree by applying the below formula:
cnt = (edges * 3) + left + right;
Step 8: Return the value
Step 9: End.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countEdges(int H)
{
int edges, right, left;
edges = 2 * (pow(2, H) - 1);
left = right = H + 1;
int cnt = (edges * 3) + left + right;
return cnt;
}
int main()
{
int H = 1;
cout << countEdges(H);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countEdges(int H)
{
int edges, right, left;
edges = 2 * (int)(Math.pow(2, H) - 1);
left = right = H + 1;
int cnt = (edges * 3) + left + right;
return cnt;
}
public static void main(String[] args)
{
int H = 1;
System.out.println(countEdges(H));
}
}
|
Python 3
def countEdges( H):
edges = 2 * (pow(2, H) - 1)
left = right = H + 1
cnt = (edges * 3) + left + right
return cnt
if __name__ == "__main__":
H = 1;
print(countEdges(H))
|
C#
using System;
class GFG
{
static int countEdges(int H)
{
int edges, right, left;
edges = 2 * (int)(Math.Pow(2, H) - 1);
left = right = H + 1;
int cnt = (edges * 3) + left + right;
return cnt;
}
public static void Main()
{
int H = 1;
Console.WriteLine(countEdges(H));
}
}
|
Javascript
<script>
function countEdges(H)
{
let edges, right, left;
edges = 2 * (Math.pow(2, H) - 1);
left = right = H + 1;
let cnt = (edges * 3) + left + right;
return cnt;
}
let H = 1;
document.write(countEdges(H));
</script>
|
Time Complexity : O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...