Number of distinct integers obtained by lcm(X, N)/X
Last Updated :
25 Aug, 2022
Given a number N, find the number of distinct integers obtained by LCM(X, N)/X where X can be any positive number.
Examples:
Input: N = 2
Output: 2
if X is 1, then lcm(1, 2)/1 is 2/1=2.
if X is 2, then lcm(2, 2)/2 is 2/2=1.
For any X greater than 2 we cannot
obtain a distinct integer.
Input: N = 3
Output: 2
It is known that LCM(x, y) = x*y/GCD(x, y).
Therefore,
lcm(X, N) = X*N/gcd(X, N)
or, lcm(X, N)/X = N/gcd(X, N)
So only the distinct factors of 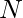 can be the distinct integers possible. Hence, count the number of distinct factors of N including 1 and N itself, which is the required answer.
can be the distinct integers possible. Hence, count the number of distinct factors of N including 1 and N itself, which is the required answer.
Below is the implementation of the above approach:
C++
#include <cmath>
#include <iostream>
using namespace std;
int numberOfDistinct(int n)
{
int ans = 0;
for (int i = 1; i <= sqrt(n); i++) {
if (n % i == 0) {
ans++;
if ((n / i) != i)
ans++;
}
}
return ans;
}
int main()
{
int n = 3;
cout << numberOfDistinct(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int numberOfDistinct(int n)
{
int ans = 0;
for (int i = 1; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
ans++;
if ((n / i) != i)
ans++;
}
}
return ans;
}
public static void main (String[] args) {
int n = 3;
System.out.println (numberOfDistinct(n));
}
}
|
Python3
import math
def numberOfDistinct(n):
ans = 0
for i in range( 1, int(math.sqrt(n))+1):
if (n % i == 0) :
ans += 1
if ((n // i) != i):
ans += 1
return ans
if __name__ == "__main__":
n = 3
print(numberOfDistinct(n))
|
C#
using System;
class GFG
{
static int numberOfDistinct(int n)
{
int ans = 0;
for (int i = 1; i <= Math.Sqrt(n); i++)
{
if (n % i == 0)
{
ans++;
if ((n / i) != i)
ans++;
}
}
return ans;
}
static public void Main ()
{
int n = 3;
Console.WriteLine(numberOfDistinct(n));
}
}
|
PHP
<?php
function numberOfDistinct($n)
{
$ans = 0;
for ($i = 1; $i <= sqrt($n); $i++)
{
if ($n % $i == 0)
{
$ans++;
if (($n / $i) != $i)
$ans++;
}
}
return $ans;
}
$n = 3;
echo numberOfDistinct($n);
?>
|
Javascript
<script>
function numberOfDistinct(n) {
var ans = 0;
for (i = 1; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
ans++;
if ((n / i) != i)
ans++;
}
}
return ans;
}
var n = 3;
document.write(numberOfDistinct(n));
</script>
|
Time Complexity: O(sqrt(n)), since there runs a loop for sqrt(n) times.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...