Number of Co-prime pairs from 1 to N with product equals to N
Last Updated :
06 May, 2021
Given a number N. The task is to find the number of co-prime pairs (a, b) from 1 to N such that their product(a*b) is equal to N.
Note: A pair(a, b) is said to be co-prime if gcd(a, b) = 1.
Examples:
Input: N = 120
Output: No. of co-prime pairs = 3
(3, 40)
(5, 24)
(8, 15)
Input: N= 250
Output: No. of co-prime pairs = 3
(2, 125)
Approach: Given that the elements in the pair should be co-prime to each other. Let a co prime pair be (a, b),
Given, a * b = N.
Therefore,
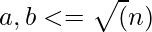
So the idea is to run a loop from 1 to 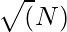 and check whether i and (N/i) are coprime to each other or not and whether, i*(N/i) = N. If yes, then count such pairs.
and check whether i and (N/i) are coprime to each other or not and whether, i*(N/i) = N. If yes, then count such pairs.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void countCoprimePairs(int n)
{
int count = 0;
cout << "The co- prime pairs are: " << endl;
for (int i = 2; i <= sqrt(n); i++) {
if (n % i == 0) {
if (__gcd(i, (n / i)) == 1) {
cout << "(" << i << ", " << (n / i) << ")\n";
count++;
}
}
}
cout << "\nNumber of coprime pairs : " << count;
}
int main()
{
int N = 120;
countCoprimePairs(N);
return 0;
}
|
Java
import java.io.*;
public class GFG {
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
static void countCoprimePairs(int n)
{
int count = 0;
System.out.println( "The co- prime pairs are: ");
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
if (__gcd(i, (n / i)) == 1) {
System.out.print( "(" +i + ", " + (n / i) + ")\n");
count++;
}
}
}
System.out.println("\nNumber of coprime pairs : " + count);
}
public static void main (String[] args) {
int N = 120;
countCoprimePairs(N);
}
}
|
Python 3
from math import *
def countCoprimePairs(n) :
count = 0
print("The co-prime pairs are: ")
for i in range(2, int(sqrt(n)) + 1) :
if n % i == 0 :
if gcd(i, n // i) == 1 :
print("(", i,",", (n // i),")")
count += 1
print("Number of coprime pairs : ", count)
if __name__ == "__main__" :
N = 120
countCoprimePairs(N)
|
C#
using System;
class GFG
{
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a - b, b);
return __gcd(a, b - a);
}
static void countCoprimePairs(int n)
{
int count = 0;
Console.WriteLine("The co- prime pairs are: ");
for (int i = 2; i <= Math.Sqrt(n); i++)
{
if (n % i == 0)
{
if (__gcd(i, (n / i)) == 1)
{
Console.WriteLine( "(" + i + ", " +
(n / i) + ")\n");
count++;
}
}
}
Console.WriteLine("\nNumber of coprime" +
" pairs : " + count);
}
public static void Main ()
{
int N = 120;
countCoprimePairs(N);
}
}
|
PHP
<?php
function gcd($a,$b)
{
return $b ? gcd($b, $a % $b) : $a;
}
function countCoprimePairs($n)
{
$count = 0;
echo "The co-prime pairs are: " ."\n";
for ($i = 2; $i <= sqrt($n); $i++)
{
if ($n % $i == 0)
{
if (gcd($i, ($n / $i)) == 1)
{
echo "(" .$i . ", " . ($n / $i) .")\n";
$count++;
}
}
}
echo "\nNumber of coprime pairs : " . $count;
}
$N = 120;
countCoprimePairs($N);
?>
|
Javascript
<script>
function __gcd(a, b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a - b, b);
return __gcd(a, b - a);
}
function countCoprimePairs(n)
{
var count = 0;
document.write( "The co- prime pairs are: " + "<br>");
for (var i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
if (__gcd(i, parseInt(n / i)) == 1) {
document.write( "(" + i + ", " + parseInt(n / i) + ")<br>");
count++;
}
}
}
document.write( "<br>Number of coprime pairs : " + count);
}
var N = 120;
countCoprimePairs(N);
</script>
|
Output: The co- prime pairs are:
(3, 40)
(5, 24)
(8, 15)
Number of coprime pairs : 3
Share your thoughts in the comments
Please Login to comment...