Minimum swaps required to bring all elements less than or equal to k together
Last Updated :
24 Mar, 2023
Given an array of n positive integers and a number k. Find the minimum number of swaps required to bring all the numbers less than or equal to k together.
Example:
Input: arr[] = {2, 1, 5, 6, 3}, k = 3
Output: 1
Explanation:
To bring elements 2, 1, 3 together, swap element ‘5’ with ‘3’ such that final array will be arr[] = {2, 1, 3, 6, 5}
Input: arr[] = {2, 7, 9, 5, 8, 7, 4}, k = 5
Output: 2
Naive Approach: A simple solution is to first count all elements less than or equal to k(say ‘good’). Now traverse for every sub-array and swap those elements whose value is greater than k. The time complexity of this approach is O(n2)
Efficient Approach: We can use the two-pointer technique and a sliding window.
- Find the count of all elements which are less than or equal to ‘k’. Let’s say the count is ‘cnt’
- Using the two-pointer technique for a window of length ‘cnt’, each time keep track of how many elements in this range are greater than ‘k’. Let’s say the total count is ‘bad’.
- Repeat step 2, for every window of length ‘cnt’ and take a minimum of count ‘bad’ among them. This will be the final answer.
Flowchart
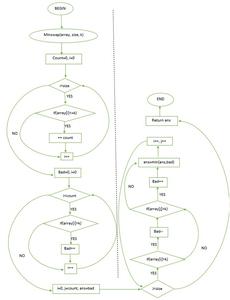
Flowchart minswap
C++
#include <iostream>
using namespace std;
int minSwap(int *arr, int n, int k) {
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
if (arr[i] > k)
--bad;
if (arr[j] > k)
++bad;
ans = min(ans, bad);
}
return ans;
}
int main() {
int arr[] = {2, 1, 5, 6, 3};
int n = sizeof(arr) / sizeof(arr[0]);
int k = 3;
cout << minSwap(arr, n, k) << "\n";
int arr1[] = {2, 7, 9, 5, 8, 7, 4};
n = sizeof(arr1) / sizeof(arr1[0]);
k = 5;
cout << minSwap(arr1, n, k);
return 0;
}
|
Java
import java.lang.*;
class GFG {
static int minSwap(int arr[], int n, int k) {
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
if (arr[i] > k)
--bad;
if (arr[j] > k)
++bad;
ans = Math.min(ans, bad);
}
return ans;
}
public static void main(String[] args)
{
int arr[] = {2, 1, 5, 6, 3};
int n = arr.length;
int k = 3;
System.out.print(minSwap(arr, n, k) + "\n");
int arr1[] = {2, 7, 9, 5, 8, 7, 4};
n = arr1.length;
k = 5;
System.out.print(minSwap(arr1, n, k));
}
}
|
Python3
def minSwap(arr, n, k) :
count = 0
for i in range(0, n) :
if (arr[i] <= k) :
count = count + 1
bad = 0
for i in range(0, count) :
if (arr[i] > k) :
bad = bad + 1
ans = bad
j = count
for i in range(0, n) :
if(j == n) :
break
if (arr[i] > k) :
bad = bad - 1
if (arr[j] > k) :
bad = bad + 1
ans = min(ans, bad)
j = j + 1
return ans
arr = [2, 1, 5, 6, 3]
n = len(arr)
k = 3
print (minSwap(arr, n, k))
arr1 = [2, 7, 9, 5, 8, 7, 4]
n = len(arr1)
k = 5
print (minSwap(arr1, n, k))
|
C#
using System;
class GFG {
static int minSwap(int []arr, int n, int k) {
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
if (arr[i] > k)
--bad;
if (arr[j] > k)
++bad;
ans = Math.Min(ans, bad);
}
return ans;
}
public static void Main()
{
int []arr = {2, 1, 5, 6, 3};
int n = arr.Length;
int k = 3;
Console.WriteLine(minSwap(arr, n, k));
int []arr1 = {2, 7, 9, 5, 8, 7, 4};
n = arr1.Length;
k = 5;
Console.WriteLine(minSwap(arr1, n, k));
}
}
|
PHP
<?php
function minSwap($arr, $n, $k)
{
$count = 0;
for ($i = 0; $i < $n; ++$i)
if ($arr[$i] <= $k)
++$count;
$bad = 0;
for ($i = 0; $i < $count; ++$i)
if ($arr[$i] > $k)
++$bad;
$ans = $bad;
for ($i = 0, $j = $count; $j < $n;
++$i, ++$j)
{
if ($arr[$i] > $k)
--$bad;
if ($arr[$j] > $k)
++$bad;
$ans = min($ans, $bad);
}
return $ans;
}
$arr = array(2, 1, 5, 6, 3);
$n = sizeof($arr);
$k = 3;
echo(minSwap($arr, $n, $k) . "\n");
$arr1 = array(2, 7, 9, 5, 8, 7, 4);
$n = sizeof($arr1);
$k = 5;
echo(minSwap($arr1, $n, $k));
?>
|
Javascript
<script>
function minSwap(arr, n, k) {
var count = 0;
for (var i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
var bad = 0;
for (var i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
var ans = bad;
for (var i = 0, j = count; j < n; ++i, ++j) {
if (arr[i] > k)
--bad;
if (arr[j] > k)
++bad;
ans = Math.min(ans, bad);
}
return ans;
}
var arr=[2, 1, 5, 6, 3];
var n =5;
var k = 3;
document.write(minSwap(arr, n, k) + "<br>");
var arr1 = [2, 7, 9, 5, 8, 7, 4];
n = 7;
k = 5;
document.write(minSwap(arr1, n, k));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Another approach for solving this problem is just using a simple Sliding window technique without using any pointers which can be done in O(N) time
- We will name our sliding window as snowballs. Our snowballs will be a number of elements less than or equal to K. Swap variable will start from 0 and we will increase its size as we encounter any element greater than K.
- If we see an element arr[i] value greater than k, we will increase the swap else we will decrease it.
- we will keep the count variable to keep track of the number of swaps and also min_count is required to store the minimum value of count.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minSwap(int arr[], int n, int k)
{
int snowBallSize = 0;
for (int i = 0; i < n; i++) {
if (arr[i] <= k) {
snowBallSize++;
}
}
int swap = 0, ans_swaps = INT_MAX;
for (int i = 0; i < snowBallSize; i++) {
if (arr[i] > k)
swap++;
}
ans_swaps = min(ans_swaps, swap);
for (int i = snowBallSize; i < n; i++) {
if (arr[i - snowBallSize] <= k && arr[i] > k)
swap++;
else if (arr[i - snowBallSize] > k && arr[i] <= k)
swap--;
ans_swaps = min(ans_swaps, swap);
}
return ans_swaps;
}
int main()
{
int arr1[] = { 2, 7, 9, 5, 8, 7, 4 };
int n = sizeof(arr1) / sizeof(arr1[0]);
int k = 5;
cout << minSwap(arr1, n, k) << "\n";
return 0;
}
|
Java
import java.io.*;
class GFG {
static int minSwap(int arr[], int n, int k)
{
int snowBallSize = 0;
for (int i = 0; i < n; i++) {
if (arr[i] <= k) {
snowBallSize++;
}
}
int swap = 0, ans_swaps = Integer.MAX_VALUE;
for (int i = 0; i < snowBallSize; i++) {
if (arr[i] > k)
swap++;
}
ans_swaps = Math.min(ans_swaps, swap);
for (int i = snowBallSize; i < n; i++) {
if (arr[i - snowBallSize] <= k && arr[i] > k)
swap++;
else if (arr[i - snowBallSize] > k
&& arr[i] <= k)
swap--;
ans_swaps = Math.min(ans_swaps, swap);
}
return ans_swaps;
}
public static void main(String[] args)
{
int arr1[] = { 2, 7, 9, 5, 8, 7, 4 };
int n = arr1.length;
int k = 5;
System.out.println(minSwap(arr1, n, k));
}
}
|
Python3
import sys
import math
class GFG :
@staticmethod
def minSwap( arr, n, k) :
snowBallSize = 0
i = 0
while (i < n) :
if (arr[i] <= k) :
snowBallSize += 1
i += 1
swap = 0
ans_swaps = sys.maxsize
i = 0
while (i < snowBallSize) :
if (arr[i] > k) :
swap += 1
i += 1
ans_swaps = min(ans_swaps,swap)
i = snowBallSize
while (i < n) :
if (arr[i - snowBallSize] <= k and arr[i] > k) :
swap += 1
elif(arr[i - snowBallSize] > k and arr[i] <= k) :
swap -= 1
ans_swaps = min(ans_swaps,swap)
i += 1
return ans_swaps
@staticmethod
def main( args) :
arr1 = [2, 7, 9, 5, 8, 7, 4]
n = len(arr1)
k = 5
print(GFG.minSwap(arr1, n, k))
if __name__=="__main__":
GFG.main([])
|
C#
using System;
public class GFG {
static int minSwap(int[] arr, int n, int k)
{
int snowBallSize = 0;
for (int i = 0; i < n; i++) {
if (arr[i] <= k) {
snowBallSize++;
}
}
int swap = 0, ans_swaps = Int32.MaxValue;
for (int i = 0; i < snowBallSize; i++) {
if (arr[i] > k)
swap++;
}
ans_swaps = Math.Min(ans_swaps, swap);
for (int i = snowBallSize; i < n; i++) {
if (arr[i - snowBallSize] <= k && arr[i] > k)
swap++;
else if (arr[i - snowBallSize] > k
&& arr[i] <= k)
swap--;
ans_swaps = Math.Min(ans_swaps, swap);
}
return ans_swaps;
}
static public void Main()
{
int[] arr1 = { 2, 7, 9, 5, 8, 7, 4 };
int n = arr1.Length;
int k = 5;
Console.WriteLine(minSwap(arr1, n, k));
}
}
|
Javascript
function minSwap(arr, n, k){
let snowBallSize = 0;
for(let i = 0; i < n; i++)
{
if (arr[i] <= k) {
snowBallSize++;
}
}
let swap = 0, ans_swaps = Number.MAX_VALUE;
for(let i = 0; i < snowBallSize; i++){
if (arr[i] > k){
swap++;
}
}
ans_swaps = Math.min(ans_swaps, swap);
for(let i = snowBallSize; i < n; i++){
if (arr[i - snowBallSize] <= k && arr[i] > k)
swap++;
else if (arr[i - snowBallSize] > k
&& arr[i] <= k)
swap--;
ans_swaps = Math.min(ans_swaps, swap);
}
return ans_swaps;
}
let arr1 = [ 2, 7, 9, 5, 8, 7, 4 ];
let n = arr1.length;
let k = 5;
console.log(minSwap(arr1, n, k));
|
PHP
<?php
function minSwap($arr, $n, $k) {
$snowBallSize = 0;
for ($i = 0; $i < $n; $i++) {
if ($arr[$i] <= $k) {
$snowBallSize++;
}
}
$swap = 0;
$ans_swaps = PHP_INT_MAX;
for ($i = 0; $i < $snowBallSize; $i++) {
if ($arr[$i] > $k)
$swap++;
}
$ans_swaps = min($ans_swaps, $swap);
for ($i = $snowBallSize; $i < $n; $i++) {
if ($arr[$i - $snowBallSize] <= $k && $arr[$i] > $k)
$swap++;
else if ($arr[$i - $snowBallSize] > $k && $arr[$i] <= $k)
$swap--;
$ans_swaps = min($ans_swaps, $swap);
}
return $ans_swaps;
}
$arr1 = array(2, 7, 9, 5, 8, 7, 4);
$n = count($arr1);
$k = 5;
echo minSwap($arr1, $n, $k) . "\n";
?>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...