Minimum number of elements to be removed to make XOR maximum
Last Updated :
31 Aug, 2022
Given a number 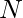 where
where 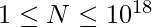 . The task is to find the minimum number of elements to be deleted in between
. The task is to find the minimum number of elements to be deleted in between 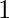 to
to 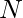 such that the XOR obtained from the remaining elements is maximum.
such that the XOR obtained from the remaining elements is maximum.
Examples:
Input: N = 5
Output: 2
Input: 1000000000000000
Output: 1
Approach: Considering the following cases:
Case 1: When 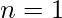 or
or  , then answer is 0. No need to remove any element.
, then answer is 0. No need to remove any element.
Case 2: Now, we have to find a number which is power of 2 and greater than or equal to 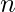 .
.
Let’s call this number be 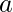 .
.
So, if  or
or 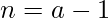 then we will just remove
then we will just remove 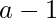 . Hence the answer is 1.
. Hence the answer is 1.
else if  , then answer is 0. No need to remove any element.
, then answer is 0. No need to remove any element.
Case 3: Otherwise, if 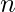 is
is 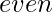 , then answer is 1.
, then answer is 1.
else if 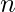 is
is 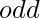 , then answer is 2.
, then answer is 2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
unsigned int nextPowerOf2(unsigned int n)
{
unsigned count = 0;
if (n && !(n & (n - 1)))
return n;
while (n != 0) {
n >>= 1;
count += 1;
}
return 1 << count;
}
int removeElement(unsigned int n)
{
if (n == 1 || n == 2)
return 0;
unsigned int a = nextPowerOf2(n);
if (n == a || n == a - 1)
return 1;
else if (n == a - 2)
return 0;
else if (n % 2 == 0)
return 1;
else
return 2;
}
int main()
{
unsigned int n = 5;
cout << removeElement(n);
return 0;
}
|
Java
public class GFG {
static int nextPowerOf2(int n)
{
int count = 0;
if (n!=0 && (n& (n - 1))==0)
return n;
while (n != 0) {
n >>= 1;
count += 1;
}
return 1 << count;
}
static int removeElement(int n)
{
if (n == 1 || n == 2)
return 0;
int a = nextPowerOf2(n);
if (n == a || n == a - 1)
return 1;
else if (n == a - 2)
return 0;
else if (n % 2 == 0)
return 1;
else
return 2;
}
public static void main(String[] args) {
int n = 5;
System.out.println(removeElement(n));
}
}
|
Python 3
def nextPowerOf2(n) :
count = 0
if (n and not(n and (n - 1))) :
return n
while n != 0 :
n >>= 1
count += 1
return 1 << count
def removeElement(n) :
if n == 1 or n == 2 :
return 0
a = nextPowerOf2(n)
if n == a or n == a - 1 :
return 1
elif n == a - 2 :
return 0
elif n % 2 == 0 :
return 1
else :
return 2
if __name__ == "__main__" :
n = 5
print(removeElement(n))
|
C#
using System;
public class GFG {
static int nextPowerOf2(int n)
{
int count = 0;
if (n!=0 && (n& (n - 1))==0)
return n;
while (n != 0) {
n >>= 1;
count += 1;
}
return 1 << count;
}
static int removeElement(int n)
{
if (n == 1 || n == 2)
return 0;
int a = nextPowerOf2(n);
if (n == a || n == a - 1)
return 1;
else if (n == a - 2)
return 0;
else if (n % 2 == 0)
return 1;
else
return 2;
}
public static void Main() {
int n = 5;
Console.Write(removeElement(n));
}
}
|
PHP
<?php
function nextPowerOf2($n)
{
$count = 0;
if ($n && !($n & ($n - 1)))
return $n;
while ($n != 0)
{
$n >>= 1;
$count += 1;
}
return 1 << $count;
}
function removeElement($n)
{
if ($n == 1 || $n == 2)
return 0;
$a = nextPowerOf2($n);
if ($n == $a || $n == $a - 1)
return 1;
else if ($n == $a - 2)
return 0;
else if ($n % 2 == 0)
return 1;
else
return 2;
}
$n = 5;
echo removeElement($n);
?>
|
Javascript
<script>
function nextPowerOf2(n)
{
let count = 0;
if (n && !(n & (n - 1)))
return n;
while (n != 0) {
n >>= 1;
count += 1;
}
return 1 << count;
}
function removeElement(n)
{
if (n == 1 || n == 2)
return 0;
let a = nextPowerOf2(n);
if (n == a || n == a - 1)
return 1;
else if (n == a - 2)
return 0;
else if (n % 2 == 0)
return 1;
else
return 2;
}
let n = 5;
document.write(removeElement(n));
</script>
|
Time complexity: O(logn)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...