Maximum Cuts in Chessboard such that it is not divided into 2 parts
Last Updated :
03 Oct, 2023
Given M x N Chessboard. The task is to determine the Maximum number of cuts that we can make in the Chessboard such that the Chessboard is not divided into 2 parts.
Examples:
Input: M = 2, N = 2
Output: Maximum cuts = 1
Explanation: We can only make 1 cut (mark in red). if we make 1 more cut then the chessboard will divide into 2 pieces.
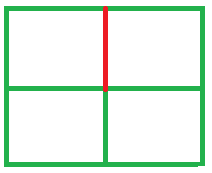
Maximum Cuts in Chessboard such that it is not divided into 2 parts( 2*2 Chessboard)
Input: M = 2, N = 4
Output: Maximum cuts = 3
Explanation: We can makes 3 cuts (marks in red). if we make 1 more cut then the chessboard will divide into 2 pieces.
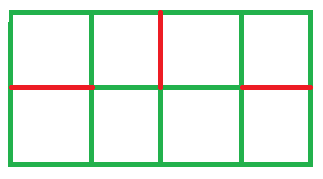
Maximum Cuts in Chessboard such that it is not divided into 2 parts( 2*4 Chessboard)
Approach:
To find the maximum number of cuts in an M x N chessboard without dividing it into two parts, it can observed that formula is (M-1) * (N-1). This approach involves making M-1 horizontal cuts and N-1 vertical cuts. Further cuts would result in dividing the chessboard into disconnected sections, so this formula provides the optimal solution for maximizing cuts while keeping the board intact.
Below is the implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int numberOfCuts(int M, int N)
{
int result = 0;
result = (M - 1) * (N - 1);
return result;
}
int main()
{
int M = 4, N = 4;
int Cuts = numberOfCuts(M, N);
cout << "Maximum cuts = " << Cuts;
return 0;
}
|
Java
class GFG {
static int numberOfCuts(int M, int N)
{
int result = 0;
result = (M - 1) * (N - 1);
return result;
}
public static void main(String args[])
{
int M = 4, N = 4;
int Cuts = numberOfCuts(M, N);
System.out.println("Maximum cuts = " + Cuts);
}
}
|
Python3
def numberOfCuts(M, N):
result = 0
result = (M - 1) * (N - 1)
return result
if __name__=='__main__':
M, N = 4, 4
Cuts = numberOfCuts(M, N)
print("Maximum cuts = ", Cuts)
|
C#
using System;
public class GFG{
static int numberOfCuts(int M, int N)
{
int result = 0;
result = (M - 1) * (N - 1);
return result;
}
static public void Main (){
int M = 4, N = 4;
int Cuts = numberOfCuts(M, N);
Console.WriteLine("Maximum cuts = " + Cuts);
}
}
|
Javascript
<script>
function numberOfCuts(M, N)
{
var result = 0;
result = (M - 1) * (N - 1);
return result;
}
var M = 4, N = 4;
var Cuts = numberOfCuts(M, N);
document.write( "Maximum cuts = " + Cuts);
</script>
|
PHP
<?php
function numberOfCuts($M, $N)
{
$result = 0;
$result = ($M - 1) * ($N - 1);
return $result;
}
$M = 4;
$N = 4;
$Cuts = numberOfCuts($M, $N);
echo "Maximum cuts = ", $Cuts ;
?>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...