Mensuration 2D Formula & Aptitude Questions
Last Updated :
10 Mar, 2023
Mensuration 2D is an important topic in Quantitative Aptitude, which mainly deals with problems related to the perimeter and area of two-dimensional shapes such as triangles, squares, rectangles, circles, parallelograms, etc. In Quantitative Aptitude, this topic does not have many variations and most of the questions are based on certain fixed formulas. The ability to quickly and accurately calculate the area and perimeter of 2D shapes is an essential skill required for various competitive exams, including aptitude tests.
It is therefore important for candidates to have a good understanding of 2D mensuration concepts and be able to apply them to solve problems
Practice Quiz:
Practice Mensuration 2D Aptitude Quiz Questions
Mensuration Important Terminologies
Terms | Unit | Definitions |
Area
| Square units
| The region enclosed by the 2D figure is called the area.
|
Perimeter
| Linear units
| The length of the boundary of a 2D figure is called the perimeter.
|
Volume
| Cubic units
| The measure of the amount of space that a three-dimensional object occupies, is usually expressed in cubic units.
|
Curved Surface Area
| Square units
| The area of the outer surface of a three-dimensional object that has a curved surface, such as a cylinder or cone.
|
Lateral Surface Area
| Square units
| The area of the outer surface of a three-dimensional object that does not include its top or bottom, such as the sides of a prism or cylinder.
|
Total Surface Area
| Square units
| The sum of the area of all the surfaces of a three-dimensional object, including its base and top.
|
Square Unit
| Square units
| A unit of measurement is used for area, where one unit is equivalent to the area of a square with sides of length 1 unit.
|
Cube Unit
| Cubic units
| A unit of measurement is used for volume, where one unit is equivalent to the volume of a cube with edges of length 1 unit.
|
Triangle
Let the three sides of the triangle be a, b and c.
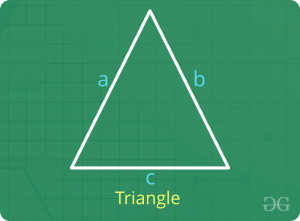
- Perimeter = a + b + c
- Area
- 2s = a + b + c
Area = 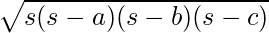
- Area = 0.5 x Base x Perpendicular Height
Rectangle
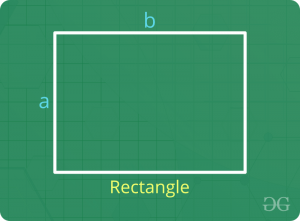
- Perimeter = 2 x (length + Breadth)
- Area = Length x Breadth
Square
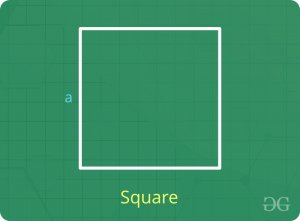
- Perimeter = 4 x Side Length
- Area = (Side Length)2 = 0.5 x (Diagonal Length)2
Parallelogram
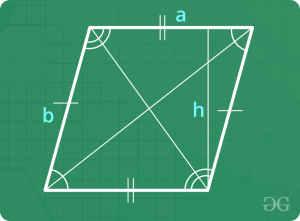
- Perimeter = 2 x Sum of adjacent sides
- Area = Base x Perpendicular Height
Rhombus
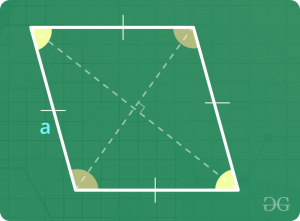
- Perimeter = 4 x Side Length
- Area = 0.5 x Product of diagonals
Trapezium
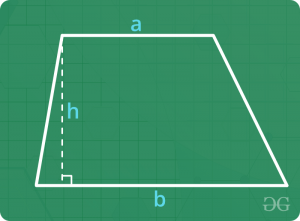
- Perimeter = Sum of all sides
- Area = 0.5 x Sum of parallel sides x Perpendicular Height
Circle
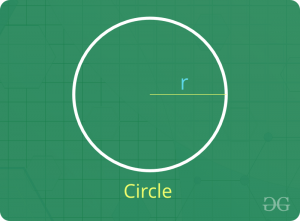
- Perimeter = 2 π Radius
- Area = π (Radius)2
- Length of an arc that subtends an angle θ at the center of the circle = (π x Radius x θ) / 180
- Area of a sector that subtends an angle θ at the center of the circle = (π x Radius2 x θ) / 360
Mensuration 2D Formulas
Shape | Area Formula (Square Units) | Perimeter Formula (Square Units) |
Square
| A = s² (where s is the length of a side)
| P = 4s (where s is the length of a side)
|
Rectangle
| A = l × w (where l is the length, w is the width)
| P = 2(l + w) (where l is the length, w is the width)
|
Circle
| A = πr² (where r is the radius)
| C = 2πr (where r is the radius)
|
Scalene Triangle
| A = (b × h) / 2 (where b is the base, h is the height)
| P = a + b + c (where a, b, and c are the lengths of the sides)
|
Isosceles Triangle
| A = (b × h) / 2 (where b is the base, h is the height)
| P = 2a + b (where a is the length of the equal sides, b is the length of the third side)
|
Equilateral Triangle
| A = (√3 / 4) × a² (where a is the length of a side)
| P = 3a (where a is the length of a side)
|
Right-Angled Triangle
| A = (b × h) / 2 (where b is the length of the base, h is the length of the height)
| P = a + b + c (where a, b, and c are the lengths of the sides)
|
Rhombus
| A = (d₁ × d₂) / 2 (where d₁ and d₂ are the lengths of the diagonals)
| P = 4s (where s is the length of a side)
|
Parallelogram
| A = b × h (where b is the base, h is the height)
| P = 2(a + b) (where a and b are the lengths of the parallel sides)
|
Trapezium
| A = ((a + b) / 2) × h (where a and b are the lengths of the parallel sides, h is the height)
| P = a + b + c + d (where a, b, c, and d are the lengths of the sides)
|
Sample Questions on Mensuration 2D
Q1: Find the perimeter and area of an isosceles triangle whose equal sides are 5 cm and height is 4 cm.
Solution:
Applying Pythagoras’ theorem,
(Hypotenuse)2 = (Base)2 + (Height)2
=> (5)2 = (0.5 x Base of isosceles triangle)2 + (4)2
=> 0.5 x Base of isosceles triangle = 3
=> Base of isosceles triangle = 6 cm
Therefore, perimeter = sum of all sides = 5 + 5 + 6 = 16 cm
Area of triangle = 0.5 x Base x Height = 0.5 x 6 x 4 = 12 cm2
Q2: A rectangular piece of dimension 22 cm x 7 cm is used to make a circle of the largest possible radius. Find the area of the circle formed.
Solution:
In questions like this, the diameter of the circle is lesser in length and breadth.
Here, the breadth Diameter of the circle = 7 cm
=> Radius of the circle = 3.5 cm
Therefore, area of the circle = π (Radius)2 = π (3.5)2 = 38.50 cm2
Q3: A pizza is to be divided into 8 identical pieces. What would be the angle subtended by each piece at the center of the circle?
Solution:
By identical pieces, we mean that area of each piece is the same.
=> Area of each piece = (π x Radius2 x θ) / 360 = (1/8) x Area of circular pizza
=> (π x Radius2 x θ) / 360 = (1/8) x (π x Radius2)
=> θ / 360 = 1 / 8
=> θ = 360 / 8 = 45
Therefore, the angle subtended by each piece at the center of the circle = 45 degrees
Q4: Four cows are tied to each corner of a square field of side 7 cm. The cows are tied with a rope such that each cow grazes the maximum possible field and all the cows graze in equal areas. Find the area of the ungrazed field.
Solution:
For maximum and equal grazing, the length of each rope has to be 3.5 cm.
=> Area grazed by 1 cow = (π x Radius2 x θ) / 360
=> Area grazed by 1 cow = (π x 3.52 x 90) / 360 = (π x 3.52) / 4
=> Area grazed by 4 cows = 4 x [(π x 3.52) / 4] = π x 3.52
=> Area grazed by 4 cows = 38.5 cm2
Now, area of square field = Side2 = 72 = 49 cm2
=> Area ungrazed = Area of field – Area grazed by 4 cows
=> Area ungrazed = 49 – 38.5 = 10.5 cm2
Q5: Find the area of the largest square that can be inscribed in a circle of radius ‘r’.
Solution:
The largest square that can be inscribed in the circle will have the diameter of the circle as the diagonal of the square.
=> Diagonal of the square = 2 r
=> Side of the square = 2 r / 21/2
=> Side of the square = 21/2 r
Therefore, area of the square = Side2 = [21/2 r]2 = 2 r2
Q6: A contractor undertakes the job of fencing a rectangular field of length 100 m and breadth 50 m. The cost of fencing is Rs. 2 per meter and the labor charges are Re. 1 per meter, both paid directly to the contractor. Find the total cost of fencing if 10 % of the amount paid to the contractor is paid as tax to the land authority.
Solution :
Total cost of fencing per meter = Rs. 2 + 1 = Rs. 3
Length of fencing required = Perimeter of the rectangular field = 2 (Length + Breadth)
=> Length of fencing required = 2 x (100 + 50) = 300 meter
=> Amount paid to the contractor = Rs. 3 x 300 = 900
=> Amount paid to the land authority = 10 % of Rs. 900 = Rs. 90
therefore, total cost of fencing = Rs. 900 + 90 = Rs. 990
Related Resources:
Problems on Mensuration 2D | Set 2
Test your knowledge of Mensuration 2D in Quantitative Aptitude with the quiz linked below, containing numerous practice questions to help you master the topic:-
<<Practice Mensuration 2D Aptitude Questions>>
Also Practice:
Share your thoughts in the comments
Please Login to comment...