Maximum number of edges that N-vertex graph can have such that graph is Triangle free | Mantel’s Theorem

Given a number N which is the number of nodes in a graph, the task is to find the maximum number of edges that N-vertex graph can have such that graph is triangle-free (which means there should not be any three edges A, B, C in the graph such that A is connected to B, B is connected to C and C is connected to A). The graph cannot contain a self-loop or multi edges.

Examples:

Input: N = 4 
Output: 4 
Explanation:

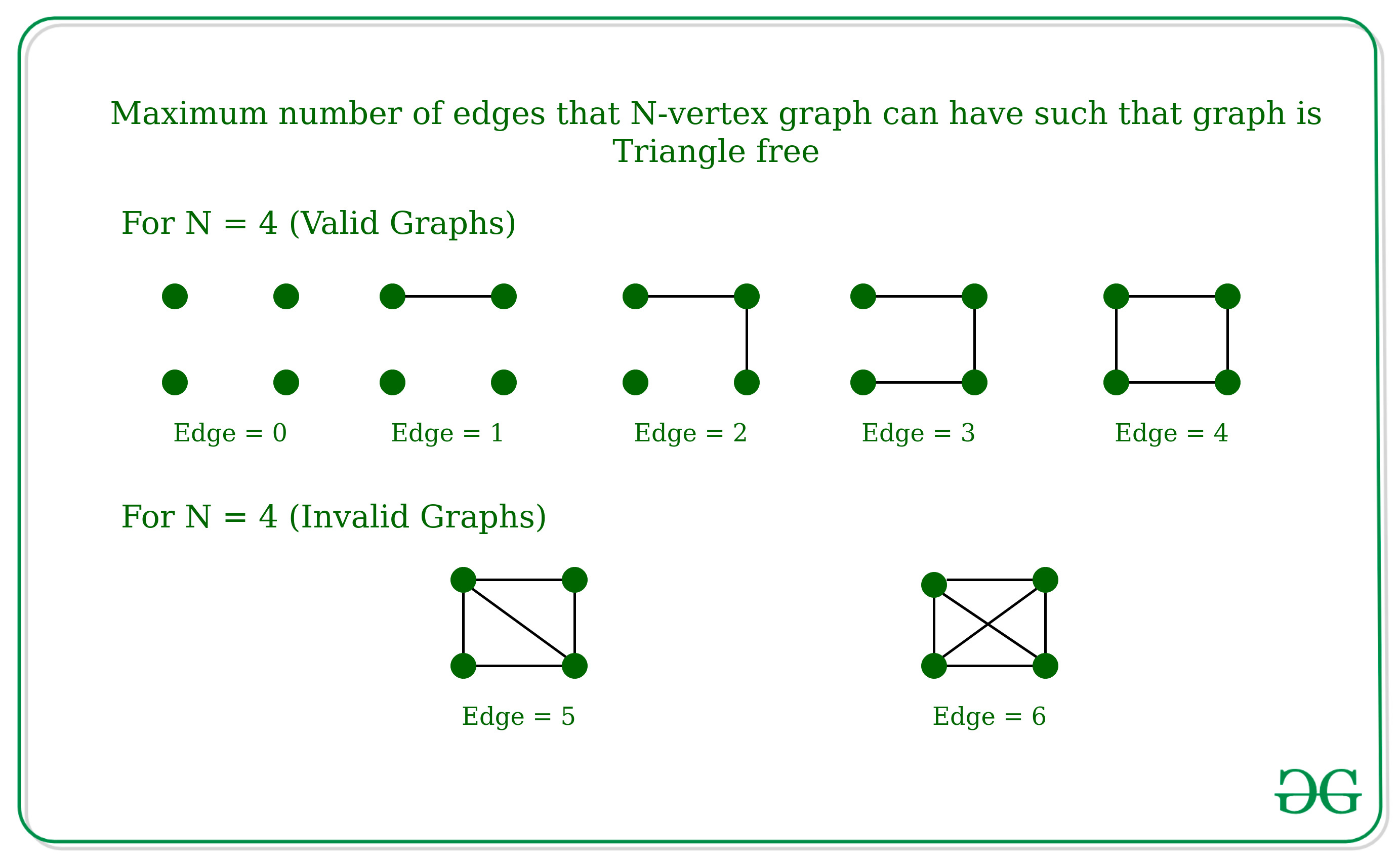
Input: N = 3 
Output: 2 
Explanation:
If there are three edges in 3-vertex graph then it will have a triangle. 

Approach: This Problem can be solved using Mantel’s Theorem which states that the maximum number of edges in a graph without containing any triangle is floor(n²/4). In other words, one must delete nearly half of the edges to obtain a triangle-free graph.

How Mantel’s Theorem Works ?
For any Graph, such that the graph is Triangle free then for any vertex Z can only be connected to any of one vertex from x and y, i.e. For any edge connected between x and y, d(x) + d(y) ? N, where d(x) and d(y) is the degree of the vertex x and y.  

• Then, the Degree of all vertex – 
  

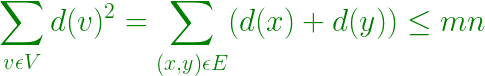
• By Cauchy-Schwarz inequality – 
  

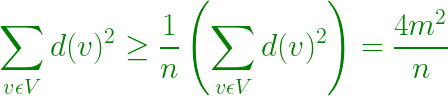
• Therefore, 4m² / n ? mn, which implies m ? n² / 4 

Below is the implementation of above approach: 

C++

// C++ implementation to find the maximum
// number of edges for triangle free graph

#include <bits/stdc++.h>
using namespace std;

// Function to find the maximum number of
// edges in a N-vertex graph.
int solve(int n)
{
    // According to the Mantel's theorem
    // the maximum number of edges will be
    // floor of [(n^2)/4]
    int ans = (n * n / 4);

    return ans;
}

// Driver Function
int main()
{
    int n = 10;
    cout << solve(n) << endl;
    return 0;
}

Java

// Java implementation to find the maximum
// number of edges for triangle free graph
class GFG
{

    // Function to find the maximum number of
    // edges in a N-vertex graph.
    public static int solve(int n)
    {

        // According to the Mantel's theorem
        // the maximum number of edges will be
        // floor of [(n^2)/4]
        int ans = (n * n / 4);

        return ans;
    }

    // Driver code
    public static void main(String args[])
    {
        int n = 10;
        System.out.println(solve(n));
    }
}

// This code is contributed by divyamohan123

C#

// C# implementation to find the maximum
// number of edges for triangle free graph
using System;

class GFG
{

    // Function to find the maximum number of
    // edges in a N-vertex graph.
    public static int solve(int n)
    {

        // According to the Mantel's theorem
        // the maximum number of edges will be
        // floor of [(n^2)/4]
        int ans = (n * n / 4);

        return ans;
    }

    // Driver code
    public static void Main()
    {
        int n = 10;
        Console.WriteLine(solve(n));
    }
}

// This code is contributed by AnkitRai01

Python3

# Python3 implementation to find the maximum
# number of edges for triangle free graph

# Function to find the maximum number of
# edges in a N-vertex graph.
def solve(n):

    # According to the Mantel's theorem
    # the maximum number of edges will be
    # floor of [(n^2)/4]
    ans = (n * n // 4)

    return ans

# Driver Function
if __name__ == '__main__':
    n = 10
    print(solve(n))

# This code is contributed by mohit kumar 29

Javascript

<script>

// Javascript implementation to find the maximum
// number of edges for triangle free graph

// Function to find the maximum number of
// edges in a N-vertex graph.
function solve(n)
{

    // According to the Mantel's theorem
    // the maximum number of edges will be
    // floor of [(n^2)/4]
    var ans = (n * n / 4);

    return ans;
}

// Driver code
var n = 10;

document.write(solve(n));

// This code is contributed by aashish1995

</script>

Output:

25

Time Complexity: O(1)