Maximum integral co-ordinates with non-integer distances
Last Updated :
22 Jun, 2022
Given a maximum limit of x – coordinate and y – coordinate, we want to calculate a set of coordinates such that the distance between any two points is a non-integer number. The coordinates (i, j) chosen should be of range 0<=i<=x and 0<=j<=y. Also, we have to maximize the set.
Examples:
Input : 4 4
Output : 0 4
1 3
2 2
3 1
4 0
Explanation : Distance between any two points
mentioned in output is not integer.
Firstly, we want to create a set, which means our set cannot contain any other point with same x’s or y’s which are used before. Well, the reason behind it is that such points which either have same x-coordinate or y-coordinate would cancel that coordinate, resulting an integral distance between them.
Example, consider points (1, 4) and (1, 5), the x-coordinate would cancel and thus, we will get and integral distance.
Secondly, we can observe that, we have only x+1 distinct i-coordinates and y+1 distinct j-coordinates. Thus, the size of the set cannot exceed min(x, y)+1.
Third observation is that we know that the diagonal elements are |i-j|*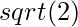 distance apart, thus, we take evaluate along the diagonal element of i-coordinate and calculate the j-coordinate by formula min(i, j)-i.
distance apart, thus, we take evaluate along the diagonal element of i-coordinate and calculate the j-coordinate by formula min(i, j)-i.
C++
#include <bits/stdc++.h>
using namespace std;
void printSet(int x, int y)
{
set<pair<int, int> > arr;
for (int i = 0; i <= min(x, y); i++) {
pair<int, int> pq;
pq = make_pair(i, min(x, y) - i);
arr.insert(pq);
}
for (auto it = arr.begin(); it != arr.end(); it++)
cout << (*it).first << " " << (*it).second << endl;
}
int main()
{
int x = 4, y = 4;
printSet(x, y);
return 0;
}
|
Java
class Pair {
public int index;
public int value;
public Pair(int index, int value)
{
this.index = index;
this.value = value;
}
}
public class Main {
static void printSet(int x, int y)
{
HashSet<String> arr = new HashSet<>();
for (int i = 0; i <= Math.min(x, y); i++) {
Pair pq = new Pair(i, Math.min(x, y) - i);
arr.add(pq.index + " " + pq.value);
}
for (String e : arr) {
System.out.println(e);
}
}
public static void main(String[] args)
{
int x = 4, y = 4;
printSet(x, y);
}
}
|
Python3
def printSet(x, y):
arr = []
for i in range(min(x, y) + 1):
pq = [i, min(x, y) - i]
arr.append(pq)
for it in arr:
print(it[0], it[1])
if __name__ == "__main__":
x = 4
y = 4
printSet(x, y)
|
C#
using System;
using System.Collections.Generic;
class Pair
{
public int index;
public int value;
public Pair(int index, int value)
{
this.index = index;
this.value = value;
}
}
public class GFG
{
static void printSet(int x, int y)
{
HashSet<String> arr = new HashSet<String>();
for (int i = 0; i <= Math.Min(x, y); i++)
{
Pair pq = new Pair(i, Math.Min(x, y) - i);
arr.Add(pq.index + " " + pq.value);
}
foreach (String e in arr)
{
Console.WriteLine(e);
}
}
public static void Main()
{
int x = 4, y = 4;
printSet(x, y);
}
}
|
Javascript
<script>
function printSet(x,y)
{
arr=[];
for (let i = 0; i <= Math.min(x, y); i++)
{
let pq = [i, Math.min(x, y) - i];
arr.push(pq);
}
for (let [key,value] of arr.entries())
{
document.write(value[0]+" "+value[1]+"<br>")
}
}
let x = 4;
let y = 4;
printSet(x, y)
</script>
|
Output:
0 4
1 3
2 2
3 1
4 0
Time Complexity: O(nlogn), where n is min(x,y) as we are using a loop to traverse min(x,y) times.
Auxiliary Space: O(n), where n is min(x,y) as we are using extra space for the set arr.
Share your thoughts in the comments
Please Login to comment...