MANOVA (Multivariate Analysis of Variance)

Last Updated : 05 Nov, 2023

A strong statistical method for evaluating the simultaneous effects of one or more independent variables on several dependent variables is a multivariate analysis of variance or MANOVA. We will look at how to use Python, a popular and flexible computer language for data analysis, for MANOVA in this tutorial. We’ll go over the theoretical foundation, applications, and real-world examples using the robust libraries available in Python.

MANOVA

The statistical technique known as multivariate analysis of variance, or MANOVA, expands the application of analysis of variance (ANOVA) to scenarios involving several dependent variables. It is an effective and adaptable instrument that is frequently used in many disciplines, such as the social sciences, biology, psychology, and Data Sciences. MANOVA facilitates the investigation and comprehension of the responses of several linked dependent variables to changes in one or more independent variables by researchers. ANOVA can only handle one dependent variable at a time; in contrast, MANOVA allows you to evaluate the combined effects of several dependent variables in a single analysis.

Finding significant differences between groups defined by the independent variables with respect to a set of dependent variables is the main objective of a MANOVA. Because of this, it is especially helpful when researchers are working with complicated data sets and need to take interdependencies between the results into consideration.

The fact that MANOVA takes into account the relationships between dependent variables—something that ANOVA is unable to do—is one of its main advantages. In doing so, it offers a more thorough comprehension of how modifications to the independent variable or variables affect the overall response pattern across the dependent variables.

Researchers use MANOVA for a variety of purposes, like evaluating the efficacy of different teaching approaches, examining how environmental factors affect several biological indicators, or determining how advertising tactics affect diverse consumer views. MANOVA is a crucial tool in the statistical toolbox of many scientific and research projects because it can help users gain deeper insights from their data by taking into account the combined impact of several variables. In later analyses, this introductory tool can serve as a springboard for investigating and deciphering more intricate interactions between variables.

A multivariate statistical technique called multivariate analysis of variance (MANOVA) is used to examine group mean differences across several dependent variables at once while accounting for correlations between the variables. You can use statsmodels or scipy libraries to perform MANOVA in the context of Python.

The variables you want to forecast are the response variables. The variables that forecast the response variables are known as predictor variables.

Let x be the independent variables.

X_i={ x_11,x₁₂, …..,x_id} where (i 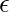$\epsilon$ N)

let y be the dependent variables.

Y_i= {y_i1, y_i2,…….,y_im}

Indicator variables are predictors for the multivariate analysis of variance (MANOVA) model as they are not quantitative variables.The model occasionally includes the trivial predictor 1.

The formula deducted from this:

$y_{i} = B^T x_{i} + \epsilon_{i}$

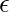Here, $\epsilon$ can also be written as $\Epsilon$ . It represents the error.

Let’s put this together and understand the formula:

$Y = BX + Error$

$Y_{nxm} = X_{nxd} B^T _{dxm} + \Epsilon_{nxm}$

$Y_{nxm} = [XB^T]_{nxm} + \Epsilon_{nxm}$

Where,

The n × m matrix:

Y = $\begin{bmatrix} y_{1,1} ...... y_{1,m}\\ y_{2,1} ...... y_{2,m}\\ y_{n,1} ...... y_{n,m} \end{bmatrix}$

There is a possibility that the n × d matrix X is not of complete rank d:

$X = \begin{bmatrix} x_{1,1} x_{1,2}......x_{1,d} \\ x_{2,1} x_{2,2}......x_{2,d} \\ x_{n,1} x_{n,2}......x_{n,d} \\ \end{bmatrix}$

The d × m matrix:

$B = \begin{bmatrix} b_{1,1} \;\; b_{1,2}......b_{1,m}\\ b_{2,1} \;\; b_{2,2}......b_{2,m}\\ b_{d,1} \;\; b_{d,2}......b_{d,m}\\ \end{bmatrix}$

The n x m matrix:

$\Epsilon = \begin{bmatrix} \epsilon_{1,1} \;\; \epsilon_{1,2} ....\epsilon_{1,m}\\ \epsilon_{2,1} \;\; \epsilon_{2,2} ....\epsilon_{2,m}\\ \epsilon_{n,1} \;\; \epsilon_{n,2} ....\epsilon_{n,m}\\ \end{bmatrix}$

Assumptions about MANOVA

Observation Independence: Each participant or observation should be independent of one another. For example, one student’s performance should not influence another’s.
Multivariate Normality: The combined dependent variables should be approximately normally distributed for each group of the independent variable.
Homogeneity of Variance-Covariance Matrices: The variance-covariance matrix of the dependent variables should be similar for all groups. This means that the spread and relationship between variables should be consistent across groups.
Absence of Multicollinearity: The dependent variables should not be too highly correlated. If two variables are very similar, it doesn’t add value to have both.
Linear Relationships: There should be a linear relationship between each pair of dependent variables for each group of the independent variable.

Remember, while these assumptions are important, real-world data often has imperfections. It’s essential to check these assumptions, and if some aren’t met, understand the implications or consider adjustments or alternative methods.

MANOVA Using Python

Setting up the Environment

Before diving into the example, ensure you have the necessary libraries. If not, install them using pip:

!pip install numpy scipy statsmodels

Let’s understand the mathematical concept with a code example.

Importing Libraries

Python3

import numpy as np
from statsmodels.multivariate.manova import MANOVA

This code imports required libraries and shows how to analyze multivariate data using MANOVA from statsmodels. This allows one to test for group differences across several dependent variables at the same time.

Defining the independent variables

Python3

X = np.random.randint(0, 100, size=(10, 5))
print('Input :\n', X)

Output:

Input :
 [[10 90 27 56 65]
 [64 69 88 34 79]
 [ 3 60 37 43 83]
 [88 70 20  6 28]
 [ 6 66 92 92 69]
 [73 54 77 21 31]
 [81 35  8 25 21]
 [45 86 16 25 37]
 [ 1  5 70 12 90]
 [74 54 78 62 72]]

Using NumPy, this code creates a random 10×5 matrix of numbers from 0 to 99. It then outputs the matrix to the terminal.

Defining the dependent variables

Python3

Y = np.random.randint(50, 300, size=(10, 3))
print('Target :\n', Y)

Output:

Target :
 [[216 103 221]
 [132 185 270]
 [115 219 116]
 [164 142 128]
 [279 269 296]
 [150 209 271]
 [228 224 143]
 [164 211  62]
 [274 283 130]
 [116 250 293]]

This code uses NumPy to create a second random 10×3 matrix of integers between 50 and 299, then outputs the matrix to the terminal.

Building MANOVA Model

Parameters in MANOVA in Python

In Python, the statsmodels library provides a function to perform MANOVA. When you use MANOVA from this library, you’ll come across some parameters that help shape the analysis. Let’s break them down in easy words:

endog: These are the outcomes you’re interested in. Imagine you’re studying student performance. This would be the scores across subjects like Math, Science, and English. It’s essentially what you’re trying to explain or understand better.
exog: These are the factors or groups you think might have an effect on the outcomes. In the student example, this could be different teaching methods or study tools used. It’s like asking, “Does using flashcards or mind maps lead to better scores across all subjects?”
missing: Sometimes, data isn’t perfect, and you might have missing values. This parameter lets you decide what to do. For example, ‘drop’ means you’ll remove any data point that has missing values.
hasconst: This checks if there’s a constant (like an intercept) in your data. Most of the time, you won’t need to worry about this. It’s more of a technical aspect that Python handles for you.

In simple words, these parameters help you tell Python, “Hey, I want to see how these groups (exog) affect these results (endog), and here’s how I want you to handle any imperfect data (missing).” The analysis then provides insights into these relationships.

Python3

# Y = XB^T+E
manova = MANOVA(endog=X,
                exog=Y)
result = manova.mv_test()
print(result.summary())

Output:

                 Multivariate linear model
============================================================
                                                            
------------------------------------------------------------
            x0           Value  Num DF Den DF F Value Pr > F
------------------------------------------------------------
           Wilks' lambda 0.4811 5.0000 3.0000  0.6473 0.6876
          Pillai's trace 0.5189 5.0000 3.0000  0.6473 0.6876
  Hotelling-Lawley trace 1.0788 5.0000 3.0000  0.6473 0.6876
     Roy's greatest root 1.0788 5.0000 3.0000  0.6473 0.6876
------------------------------------------------------------
                                                            
------------------------------------------------------------
            x1           Value  Num DF Den DF F Value Pr > F
------------------------------------------------------------
           Wilks' lambda 0.2140 5.0000 3.0000  2.2033 0.2740
          Pillai's trace 0.7860 5.0000 3.0000  2.2033 0.2740
  Hotelling-Lawley trace 3.6721 5.0000 3.0000  2.2033 0.2740
     Roy's greatest root 3.6721 5.0000 3.0000  2.2033 0.2740
------------------------------------------------------------
                                                            
------------------------------------------------------------
           x2            Value  Num DF Den DF F Value Pr > F
------------------------------------------------------------
          Wilks' lambda  0.0541 5.0000 3.0000 10.4899 0.0407
         Pillai's trace  0.9459 5.0000 3.0000 10.4899 0.0407
 Hotelling-Lawley trace 17.4832 5.0000 3.0000 10.4899 0.0407
    Roy's greatest root 17.4832 5.0000 3.0000 10.4899 0.0407
============================================================

This code first defines the relationship between the dependent variable (X) and independent variable (Y) in order to set up a MANOVA study using statsmodels. It then uses mv test() to perform a multivariate test and prints the test results summary to the console.

Key Concepts in MANOVA

Multivariate Response: Unlike ANOVA that looks at one dependent variable, MANOVA evaluates multiple dependent variables. Imagine trying to see if diet affects both weight and blood pressure. Instead of two separate tests, MANOVA assesses them together.
Dependent and Independent Variables: The dependent variables are the outcomes we’re studying (like weight and blood pressure). The independent variable, often categorical, is what might influence these outcomes (like different diets).
Group Differences: The main goal of MANOVA is to find out if there are significant differences between groups. For example, does one diet lead to greater changes in both weight and blood pressure compared to other diets?
Covariance Structures: One of the cool things about MANOVA is that it doesn’t just look at the differences in the average scores between groups. It also considers how these scores move together. This relationship is called covariance.
Pillai’s Trace, Wilks’ Lambda, Hotelling’s Trace, Roy’s Largest Root: These are fancy names for statistics that help judge if group differences are significant. Each has its strengths, and the choice often depends on the data and research question.
Assumptions: Like other tests, MANOVA works best when certain conditions are met. These include having no outliers, linear relationships between dependent variables, and more.

In short, MANOVA is like a detective tool. It helps researchers spot differences across multiple outcomes when they’re considering different groups or conditions. It’s thorough and considers both the average scores and how these scores behave together.

Real Life Applications of MANOVA

In this educational scenario, students’ performance in three subjects—mathematics, science, and history—is being assessed by the school using Multivariate Analysis of Variance (MANOVA) to compare the effects of three alternative teaching approaches: Traditional, E-Learning, and Blended.The school intends to use MANOVA to ascertain whether there is a statistically significant difference in student performance when taking into account all three subjects collectively, as opposed to examining them separately. This method considers the potential interdependence and innate relationships amongst the three subjects.

For example, a student’s success in one topic might be correlated with their performance in another, and MANOVA can handle this link. It makes it possible for the school to evaluate how different teaching strategies affect students’ academic achievement over the course of various disciplines.

The school will get important insights into which teaching strategy, if any, is more successful in promoting overall student achievement in mathematics, science, and history thanks to the results of the MANOVA analysis. It enables a thorough understanding of the cumulative influence of instructional approaches on academic outcomes, going beyond a mere comparison of means. Future curricular choices and instructional practices can be informed by this data, which will eventually help both teachers and students.

Implementing MANOVA in Python

Let’s learn how to implement MANOVA in Python:

Importing Libraries

Python

# Import necessary libraries
import pandas as pd
from statsmodels.multivariate.manova import MANOVA
from sklearn.datasets import load_iris

In this section, we import the required libraries. pandas is a popular data manipulation library, statsmodels provides tools for statistical models, and sklearn.datasets is where the iris dataset is loaded from. By importing these, we set the foundation to handle, analyze, and load our data.

Loading Dataset

Python

# Load the iris dataset
data = load_iris()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['species'] = data.target
print(df.head())

Output:

   sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)  \
0                5.1               3.5                1.4               0.2   
1                4.9               3.0                1.4               0.2   
2                4.7               3.2                1.3               0.2   
3                4.6               3.1                1.5               0.2   
4                5.0               3.6                1.4               0.2   
   species  
0        0  
1        0  
2        0  
3        0  
4        0

Here, we load the iris dataset using the load_iris() function. This dataset contains information about three species of iris flowers and their respective measurements. We then convert this data into a DataFrame (df), which is a tabular data structure provided by pandas. The columns of this DataFrame are the flower measurements, and we add an additional ‘species’ column that represents the species of each flower.

Column Renaming

Python

# Rename columns to remove spaces
df.columns = ['sepal_length', 'sepal_width',
              'petal_length', 'petal_width', 'species']

Column names with spaces can cause issues when running statistical models. To avoid this, we rename the columns by replacing spaces with underscores. This makes the column names more manageable for subsequent steps, ensuring that our statistical tests won’t run into syntax errors.

Target Label Replacement

Python

# Replace target numbers with their respective names for clarity in results
df['species'] = df['species'].map(
    {0: 'setosa', 1: 'versicolor', 2: 'virginica'})

The iris dataset originally labels species as numbers (0, 1, 2). For better clarity and interpretation of results, we replace these numeric codes with the actual species names. The map function is used to achieve this, converting each number to its corresponding species name.

Implementing MANOVA

Python

# Apply MANOVA with the renamed columns
manova = MANOVA.from_formula('sepal_length + sepal_width + petal_length + petal_width ~ species', data=df)
result = manova.mv_test()
print(result)

Output:

                   Multivariate linear model
================================================================
                                                                
----------------------------------------------------------------
       Intercept         Value  Num DF  Den DF   F Value  Pr > F
----------------------------------------------------------------
          Wilks' lambda  0.0170 4.0000 144.0000 2086.7720 0.0000
         Pillai's trace  0.9830 4.0000 144.0000 2086.7720 0.0000
 Hotelling-Lawley trace 57.9659 4.0000 144.0000 2086.7720 0.0000
    Roy's greatest root 57.9659 4.0000 144.0000 2086.7720 0.0000
----------------------------------------------------------------
                                                                
----------------------------------------------------------------
        species          Value  Num DF  Den DF   F Value  Pr > F
----------------------------------------------------------------
          Wilks' lambda  0.0234 8.0000 288.0000  199.1453 0.0000
         Pillai's trace  1.1919 8.0000 290.0000   53.4665 0.0000
 Hotelling-Lawley trace 32.4773 8.0000 203.4024  582.1970 0.0000
    Roy's greatest root 32.1919 4.0000 145.0000 1166.9574 0.0000
================================================================

Let’s understand some terms :

Wilks’ lambda: One multivariate statistical test that is employed in MANOVA to evaluate the significance of group differences across several dependent variables is Wilks’ Lambda. It gauges the amount of data volatility not attributable to group membership. A test’s p-value aids in determining statistical significance, and a lower Wilks’ Lambda value suggests more evidence of group differences.
Pillai’s trace: When doing a multivariate statistical test in MANOVA to evaluate the significance of group differences across several dependent variables, Pillai’s Trace is utilized. Measured by group membership, it represents the cumulative variance explained. When determining statistical significance, a test’s p-value is helpful in determining the size of the Pillai’s Trace, which shows greater evidence of group differences.
Hotelling-Lawley trace: A multivariate statistical test called the Hotelling-Lawley Trace is employed in MANOVA to evaluate the significance of group differences among various dependent variables. It assesses the proportion of variance explained by group membership to variance overall. Greater evidence of group differences is indicated by a larger Hotelling-Lawley Trace, and the test’s p-value aids in determining statistical significance.
Roy’s greatest root: A multivariate statistical test called Roy’s Greatest Root is employed in MANOVA to evaluate the significance of group differences among several dependent variables. The test statistic matrix’s greatest eigenvalue is assessed. Greater evidence of group differences is indicated by a greater Roy’s Greatest Root, and the test’s accompanying p-value aids in determining statistical significance.

The output will display a detailed summary of the MANOVA test, including the test statistic values (Pillai’s trace, Wilks’ lambda, etc.) and their associated p-values. If the p-values are below a chosen significance level (e.g., 0.05), you would reject the null hypothesis and conclude that there are significant differences in the multivariate response among the species.In the final section, we apply the MANOVA test. The formula indicates that we’re examining the differences in flower measurements across different species. The MANOVA.from_formula function is used to specify this relationship, and then mv_test() is called to run the test. Finally, we print the results to see if there are statistically significant differences in measurements across species. This output provides insight into how different species might vary in terms of their physical characteristics.

Advantages of MANOVA

In statistical analysis, Multivariate Analysis of Variance (MANOVA) provides a number of advantages. They are:

Simultaneous Testing: By enabling you to compare many dependent variables at once, MANOVA can help lower the possibility of Type I errors that might arise from running individual univariate tests for each variable.
Efficiency: It effectively condenses intricate correlations between several independent and dependent variables, assisting in the identification of interactions that univariate testing would overlook.
Reduction of Experiement-Wide Error Rate: MANOVA maintains statistical power by controlling experiment-wise error rates more efficiently by taking into account all dependent variables collectively.
Improved Interpretability: A deeper comprehension of the data and underlying patterns can be facilitated by using MANOVA, which can shed light on the linkages and interactions between variables.

Disadvantages of MANOVA

Although multivariate analysis of variance (MANOVA) is a potent statistical approach, it has drawbacks and limitations just like any other technique. The following are a few drawbacks of MANOVA:

Assumption Stringency: The assumptions of MANOVA are linearity, homogeneity of variance-covariance matrices between groups, and multivariate normality. Results that are not trustworthy may arise from breaking these presumptions.
Complexity: Performing and interpreting a MANOVA can be challenging, particularly for researchers who are not familiar with multivariate statistics. It necessitates a solid grasp of the data and the methodology.
Difficulty in Post-Hoc Testing: Because several dependent variables in a MANOVA are interdependent, doing post-hoc tests might be difficult. It may be challenging to determine which particular group differences are noteworthy due to this intricacy.
Multiple Testing: If necessary adjustments are not done, there is a higher chance of Type I errors (false positives) when analyzing the impact of several independent variables or performing post-hoc testing.pyt

Conclusion

To sum up, Multivariate Analysis of Variance (MANOVA) is a strong and adaptable statistical technique that provides insightful information on the connections between a number of dependent variables and one or more independent variables. A more thorough knowledge of group differences and treatment effects in research and data analysis is provided by MANOVA, which takes into account the interdependencies among these variables. When working with complex data sets where numerous factors may jointly influence the outcomes, this technique is quite helpful. MANOVA is a popular option in many fields, including psychology, education, healthcare, and more, since it makes it easy for researchers to assess the overall effect of categorical predictors on a group of linked dependent variables.

The assumptions and restrictions of MANOVA, such as the need for multivariate normality and homogeneity of variance-covariance matrices, must be understood, though. These elements should be taken into account when employing MANOVA since they may have an impact on the results’ validity.In conclusion, MANOVA is a useful tool for researchers looking to learn more about the connections between various factors. It enables them to make defensible choices, come to significant findings, and expand their knowledge in the domains in which they work.

Suggest improvement

Real Life Applications of Variance

Share your thoughts in the comments

MANOVA (Multivariate Analysis of Variance)

MANOVA

Assumptions about MANOVA

MANOVA Using Python

Setting up the Environment

Python3

Python3

Python3

Building MANOVA Model

Parameters in MANOVA in Python

Python3

Key Concepts in MANOVA

Real Life Applications of MANOVA

Implementing MANOVA in Python

Importing Libraries

Python

Loading Dataset

Python

Column Renaming

Python

Target Label Replacement

Python

Implementing MANOVA

Python

Advantages of MANOVA

Disadvantages of MANOVA

Conclusion

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?