Level order traversal in spiral form | Using one stack and one queue
Last Updated :
26 Aug, 2022
Write a function to print spiral order traversal of a tree. For below tree, function should print 1, 2, 3, 4, 5, 6, 7.
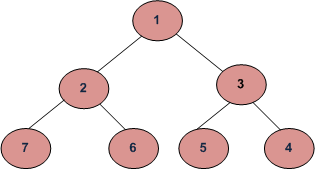
You are allowed to use only one stack.
We have seen recursive and iterative solutions using two stacks . In this post, a solution with one stack and one queue is discussed. The idea is to keep on entering nodes like normal level order traversal, but during printing, in alternative turns push them onto the stack and print them, and in other traversals, just print them the way they are present in the queue.
Following is the implementation of the idea.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* newNode(int val)
{
Node* new_node = new Node;
new_node->data = val;
new_node->left = new_node->right = NULL;
return new_node;
}
void printSpiralUsingOneStack(Node* root)
{
if (root == NULL)
return;
stack<int> s;
queue<Node*> q;
bool reverse = true;
q.push(root);
while (!q.empty()) {
int size = q.size();
while (size) {
Node* p = q.front();
q.pop();
if (reverse)
s.push(p->data);
else
cout << p->data << " ";
if (p->left)
q.push(p->left);
if (p->right)
q.push(p->right);
size--;
}
if (reverse) {
while (!s.empty()) {
cout << s.top() << " ";
s.pop();
}
}
reverse = !reverse;
}
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
printSpiralUsingOneStack(root);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class Node
{
int data;
Node left, right;
};
static Node newNode(int val)
{
Node new_node = new Node();
new_node.data = val;
new_node.left = new_node.right = null;
return new_node;
}
static void printSpiralUsingOneStack(Node root)
{
if (root == null)
return;
Stack<Integer> s = new Stack<Integer>();
Queue<Node> q = new LinkedList<Node>();
boolean reverse = true;
q.add(root);
while (!q.isEmpty())
{
int size = q.size();
while (size > 0)
{
Node p = q.peek();
q.remove();
if (reverse)
s.add(p.data);
else
System.out.print(p.data + " ");
if (p.left != null)
q.add(p.left);
if (p.right != null)
q.add(p.right);
size--;
}
if (reverse)
{
while (!s.empty())
{
System.out.print(s.peek() + " ");
s.pop();
}
}
reverse = !reverse;
}
}
public static void main(String[] args)
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
printSpiralUsingOneStack(root);
}
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.left = self.right = None
def newNode(val):
new_node = Node(0)
new_node.data = val
new_node.left = new_node.right = None
return new_node
def printSpiralUsingOneStack(root):
if (root == None):
return
s = []
q = []
reverse = True
q.append(root)
while (len(q) > 0) :
size = len(q)
while (size > 0) :
p = q[0]
q.pop(0)
if (reverse):
s.append(p.data)
else:
print( p.data ,end = " ")
if (p.left != None):
q.append(p.left)
if (p.right != None):
q.append(p.right)
size = size - 1
if (reverse) :
while (len(s)) :
print( s[-1],end= " ")
s.pop()
reverse = not reverse
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(7)
root.left.right = newNode(6)
root.right.left = newNode(5)
root.right.right = newNode(4)
printSpiralUsingOneStack(root)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class Node
{
public int data;
public Node left, right;
};
static Node newNode(int val)
{
Node new_node = new Node();
new_node.data = val;
new_node.left = new_node.right = null;
return new_node;
}
static void printSpiralUsingOneStack(Node root)
{
if (root == null)
return;
Stack<int> s = new Stack<int>();
Queue<Node> q = new Queue<Node>();
Boolean reverse = true;
q.Enqueue(root);
while (q.Count != 0)
{
int size = q.Count;
while (size > 0)
{
Node p = q.Peek();
q.Dequeue();
if (reverse)
s.Push(p.data);
else
Console.Write(p.data + " ");
if (p.left != null)
q.Enqueue(p.left);
if (p.right != null)
q.Enqueue(p.right);
size--;
}
if (reverse)
{
while (s.Count != 0)
{
Console.Write(s.Peek() + " ");
s.Pop();
}
}
reverse = !reverse;
}
}
public static void Main(String[] args)
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
printSpiralUsingOneStack(root);
}
}
|
Javascript
<script>
class Node
{
constructor()
{
this.data = 0;
this.left = null;
this.right = null;
}
};
function newNode(val)
{
var new_node = new Node();
new_node.data = val;
new_node.left = new_node.right = null;
return new_node;
}
function printSpiralUsingOneStack(root)
{
if (root == null)
return;
var s = [];
var q = [];
var reverse = true;
q.push(root);
while (q.length != 0)
{
var size = q.length;
while (size > 0)
{
var p = q[0];
q.shift();
if (reverse)
s.push(p.data);
else
document.write(p.data + " ");
if (p.left != null)
q.push(p.left);
if (p.right != null)
q.push(p.right);
size--;
}
if (reverse)
{
while (s.length != 0)
{
document.write(s[s.length - 1] + " ");
s.pop();
}
}
reverse = !reverse;
}
}
var root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(7);
root.left.right = newNode(6);
root.right.left = newNode(5);
root.right.right = newNode(4);
printSpiralUsingOneStack(root);
</script>
|
Complexity Analysis:
- Time Complexity : O(n)
- Auxiliary Space : O(n)
Share your thoughts in the comments
Please Login to comment...