Legendre’s Conjecture
Last Updated :
13 Nov, 2022
It says that there is always one prime number between any two consecutive natural number’s(n = 1, 2, 3, 4, 5, …) square. This is called Legendre’s Conjecture.
Conjecture: A conjecture is a proposition or conclusion based upon incomplete information to which no proof has been found i.e it has not been proved or disproved.
Mathematically,
there is always one prime p in the range 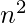 to
to 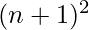 where n is any natural number.
where n is any natural number.
for examples-
2 and 3 are the primes in the range 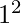 to
to 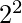 .
.
5 and 7 are the primes in the range 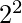 to
to 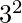 .
.
11 and 13 are the primes in the range 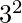 to
to 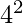 .
.
17 and 19 are the primes in the range 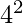 to
to 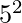 .
.
Examples:
Input : 4
output: Primes in the range 16 and 25 are:
17
19
23
Explanation: Here 42 = 16 and 52 = 25
Hence, prime numbers between 16 and 25 are 17, 19 and 23.
Input : 10
Output: Primes in the range 100 and 121 are:
101
103
107
109
113
C++
#include <bits/stdc++.h>
using namespace std;
bool isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
void LegendreConjecture(int n)
{
cout << "Primes in the range "<<n*n
<< " and "<<(n+1)*(n+1)
<<" are:" <<endl;
for (int i = n*n; i <= ((n+1)*(n+1)); i++)
if (isprime(i))
cout << i <<endl;
}
int main()
{
int n = 50;
LegendreConjecture(n);
return 0;
}
|
Java
class GFG {
static boolean isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
static void LegendreConjecture(int n)
{
System.out.println("Primes in the range "+n*n
+" and "+(n+1)*(n+1)
+" are:");
for (int i = n*n; i <= ((n+1)*(n+1)); i++)
{
if (isprime(i))
System.out.println(i);
}
}
public static void main(String[] args)
{
int n = 50;
LegendreConjecture(n);
}
}
|
Python3
import math
def isprime( n ):
i = 2
for i in range (2, int((math.sqrt(n)+1))):
if n%i == 0:
return False
return True
def LegendreConjecture( n ):
print ( "Primes in the range ", n*n
, " and ", (n+1)*(n+1)
, " are:" )
for i in range (n*n, (((n+1)*(n+1))+1)):
if(isprime(i)):
print (i)
n = 50
LegendreConjecture(n)
|
C#
using System;
class GFG {
static Boolean isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
static void LegendreConjecture(int n)
{
Console.WriteLine("Primes in the range "
+ n * n + " and " + (n + 1) * (n + 1)
+ " are:");
for (int i = n * n; i <= ((n + 1)
* (n + 1)); i++)
{
if (isprime(i))
Console.WriteLine(i);
}
}
public static void Main(String[] args)
{
int n = 50;
LegendreConjecture(n);
}
}
|
PHP
<?php
function isprime($n)
{
for ($i = 2; $i * $i <= $n; $i++)
if ($n % $i == 0)
return false;
return true;
}
function LegendreConjecture($n)
{
echo "Primes in the range ",$n* $n,
" and ",($n + 1) * ($n + 1),
" are:\n" ;
for ($i = $n * $n; $i <= (($n + 1) *
($n + 1)); $i++)
if (isprime($i))
echo $i ,"\n";
}
$n = 50;
LegendreConjecture($n);
?>
|
Javascript
<script>
function isprime(n)
{
for(let i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
function LegendreConjecture(n)
{
document.write("Primes in the range " +
n * n + " and " +
(n + 1) * (n + 1) +
" are:" + "<br/>");
for(let i = n * n;
i <= ((n + 1) * (n + 1));
i++)
{
if (isprime(i))
document.write(i + "<br/>");
}
}
let n = 50;
LegendreConjecture(n);
</script>
|
Output :
Primes in the range 2500 and 2601 are:
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593
Time Complexity: O(n2). isPrime() function takes O(n) time and it is embedded in LegendreConjecture() function which also takes O(n) time as it has loop which starts from n2 and ends at
(n+1)2 so, (n+1)2 – n2 = 2n+1.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...