Python Program for Legendre’s Conjecture
Last Updated :
27 Jul, 2023
It says that there is always one prime number between any two consecutive natural number\’s(n = 1, 2, 3, 4, 5, …) square. This is called Legendre’s Conjecture. Conjecture: A conjecture is a proposition or conclusion based upon incomplete information to which no proof has been found i.e it has not been proved or disproved.
Mathematically, there is always one prime p in the range 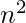 to
to 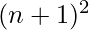 where n is any natural number. for examples- 2 and 3 are the primes in the range
where n is any natural number. for examples- 2 and 3 are the primes in the range 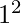 to
to 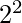 . 5 and 7 are the primes in the range
. 5 and 7 are the primes in the range 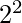 to
to 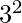 . 11 and 13 are the primes in the range
. 11 and 13 are the primes in the range 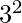 to
to 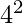 . 17 and 19 are the primes in the range
. 17 and 19 are the primes in the range 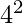 to
to 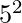 .
.
Examples:
Input : 4
output: Primes in the range 16 and 25 are:
17
19
23
Explanation: Here 42 = 16 and 52 = 25 Hence, prime numbers between 16 and 25 are 17, 19 and 23.
Input : 10
Output: Primes in the range 100 and 121 are:
101
103
107
109
113
Python3
import math
def isprime( n ):
i = 2
for i in range (2, int((math.sqrt(n)+1))):
if n%i == 0:
return False
return True
def LegendreConjecture( n ):
print ( "Primes in the range ", n*n
, " and ", (n+1)*(n+1)
, " are:" )
for i in range (n*n, (((n+1)*(n+1))+1)):
if(isprime(i)):
print (i)
n = 50
LegendreConjecture(n)
|
Output :
Primes in the range 2500 and 2601 are:
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593
Time Complexity: O(n*sqrtn). isPrime() function takes O(n) time and it is embedded in LegendreConjecture() function which also takes O(n) time as it has loop which starts from n2 and ends at
(n+1)2 so, (n+1)2 – n2 = 2n+1.
Auxiliary Space: O(1)
METHOD 2:
Instead of iterating through a range of numbers to check for prime numbers, the new approach uses the sympy library to generate all prime numbers in a given range.
- The sympy library provides the primesieve function, which takes two arguments: the start and end values for the range to search for primes.
- The primesieve function returns a generator object that can be iterated over to get all the prime numbers in the specified range.
- The isprime function is no longer necessary, as the primesieve function has already generated all prime numbers in the range.
- The LegendreConjecture function remains the same, except for the for loop, which now iterates over the prime numbers.
NOTE: First you will have to install the sympy library using the following command: pip install sympy
Python3
import sympy
def LegendreConjecture(n):
primes = list(sympy.primerange(n*n, (n+1)*(n+1)))
print(f"Primes in the range {n*n} and {(n+1)*(n+1)} are:\n")
for i in range(len(primes)):
print(primes[i])
n = 50
LegendreConjecture(n)
|
Output :
Primes in the range 2500 and 2601 are:
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593
Time complexity: O(n log log n), as the sieve of Eratosthenes algorithm has a time complexity of O(n log log n) for finding all primes up to n, and the algorithm used here is a modified version of the sieve of Eratosthenes.
Auxiliary Space: O(n), because the algorithm uses a boolean list of size n+1 to keep track of whether each number is prime or not.
Please refer complete article on Legendre’s Conjecture for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...