Left Hand And Right Hand Derivatives

Last Updated : 20 Mar, 2024

Left and Right Hand Derivatives are types of One-Sided Derivatives, representing the rate of change of a function at a specific point from either the left or the right side, respectively. They are used to analyze whether or not a function is differentiable at certain points. These derivatives provide insight into the behavior of a function locally, that helps in understanding its overall characteristics. In this article, we will discuss both Left and Right Hand Derivatives in detail, including their definitions and properties.

Table of Content

What are Derivatives?
Right-Hand Derivative(RHD) Definition
Left-Hand Derivative (LHD) Definition
Conclusion
Practice problems
Left Hand And Right Hand Derivatives: FAQ’s

What are Derivatives?

Derivatives are a fundamental concept in calculus that describe the rate of change of a function with respect to its independent variable. In simpler terms, a derivative measures how a function’s output changes as its input changes.

Derivative also defined as Slope of the tangent line to a curve at a point. For a function f(x), the derivative is denoted by $f'(x)$ ,

$\bold{f'(x)=\frac{d}{dx}[f(x)]=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}}$

What is a One-Sided Derivative?

One-sided derivative refers to the derivative of a function at a point where the function may only be defined on one side of that point. A function y= f(x) is differentiable on a closed interval [a, b], To find the derivative of f(x) at a particular point that lies in between this closed interval and the limit that exists at endpoints using,

Right-Hand Derivative OR f'(x⁺)
Left-Hand Derivative OR f'(x^–)

Figure below showing the left and Right- hand derivative of the function f(x) at x=0,

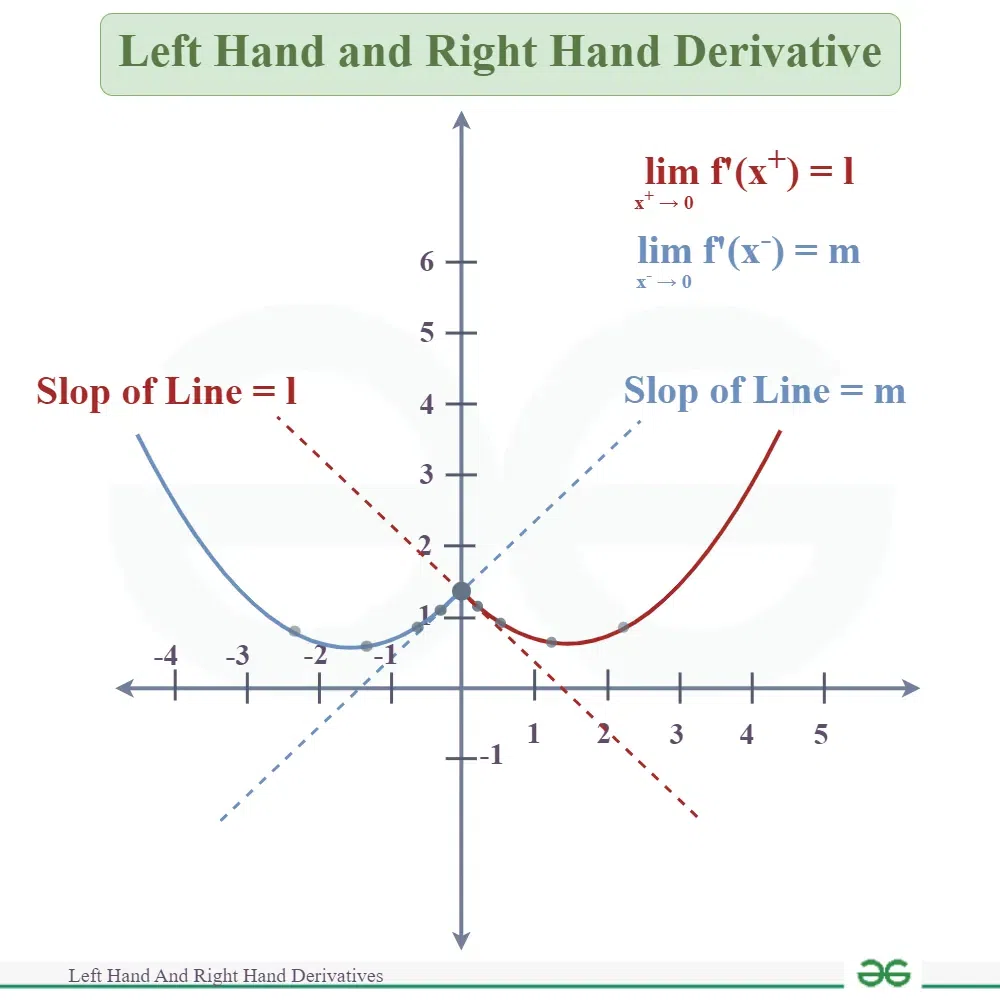
LHD and RHD of any Function at x = 0

Right-Hand Derivative(RHD) Definition

Right-hand derivative or One-sided derivative is finding the derivative of a function at a point from the Right-hand side. The Right-hand derivative is denoted by f'(a⁺).

Right-Hand-Derivative

Right-Hand Derivative Formula

For a function y=f(x), to find the Right hand derivative of f(x) at point ‘a’ is,

$\bold{f'(a^{+})=\lim_{h \rightarrow 0}\frac{f(a+h)-f(a)}{h}}$

Note: If both the right-hand and left-hand derivatives exist and are equal, then the derivative of the function f(x) at x = a exists.

Let’s consider an example for better understanding.

Let’s take the function f(x) = |x| , which represents the absolute value of x.

As we know, $|x| = \begin{cases} x, & x\geq 0 \\ -x, & x <0 \end{cases}$

For x > 0, f(x) = x, so the function is decreasing.

Thus, $f'(0^+) = \lim_{h \to 0^+ } \frac{f(0 + h) - f(0)}{h}$

$\Rightarrow f'(0^+) = \lim_{h \to 0^+} \frac{|0 + h| - |0|}{h}$

$\Rightarrow f'(0^+) = \lim_{h \to 0} \frac{|h|}{h}$

$\Rightarrow f'(0^-) = \lim_{h \to 0^-} \frac{h}{h} = 1$

So, the left-hand derivative of f(x) = |x| at x = 0 is -1 . This indicates that the function has a negative slope as x approaches 0 from the left side.

Left-Hand Derivative (LHD) Definition

Right-hand derivative represents the rate of change of the function as x approaches a point from the right-hand side.

The left-hand derivative is denoted by f'(a^–). It is also called one-sided derivative from left side.

Left-Hand-Derivative

Left-Hand Derivative Formula

For a function y=f(x), to find the left hand derivative of f(x) at point ‘a’ is,

$\bold{f'(a^{-})=\lim_{h \rightarrow 0^-}\frac{f(a-h)-f(a)}{-h}}$

Let’s consider an example for better understanding.

Let’s take the function f(x) = |x| , which represents the absolute value of x.

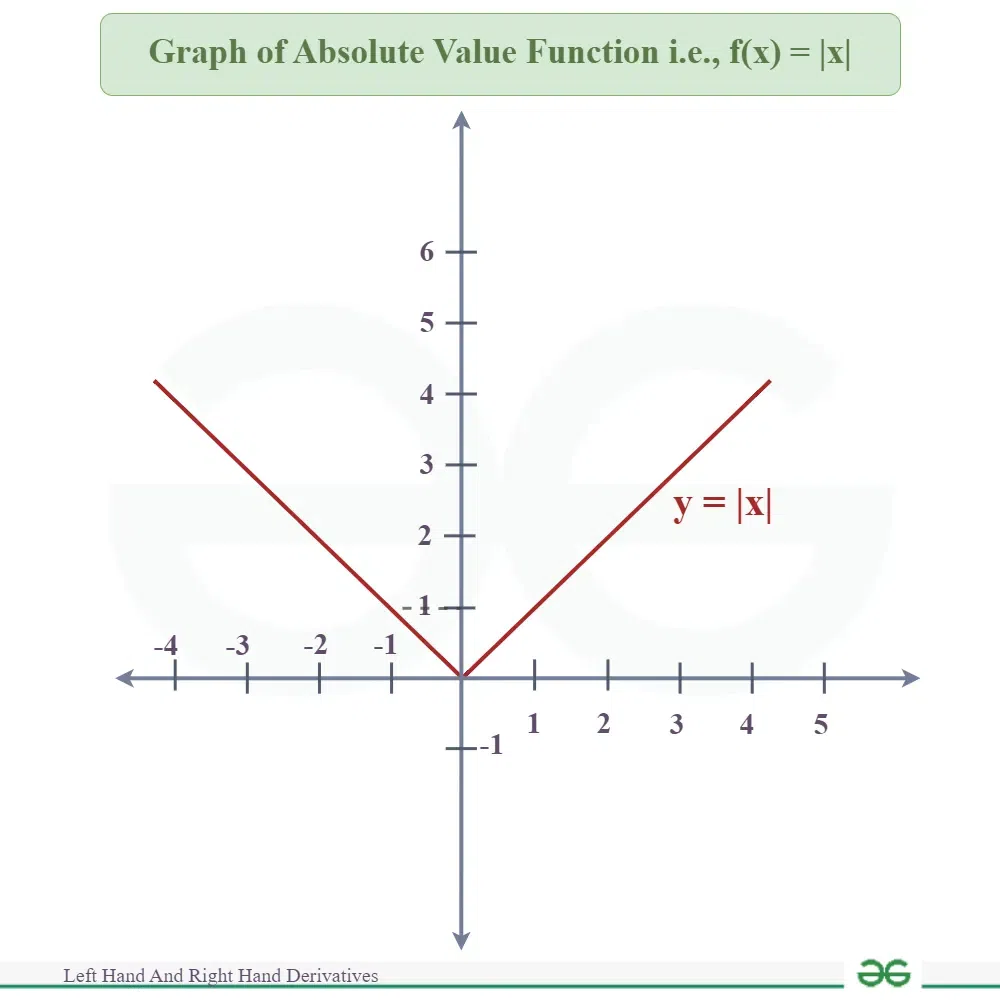
As we know, $|x| = \begin{cases} x, & x\geq 0 \\ -x, & x <0 \end{cases}$

For x < 0, f(x) = -x, so the function is decreasing.

Thus, $f'(0^-) = \lim_{h \to 0^-} \frac{f(0 - h) - f(0)}{-h}$

$\Rightarrow f'(0^-) = \lim_{h \to 0^-} \frac{|0 - h| - |0|}{-h}$

$\Rightarrow f'(0^-) = \lim_{h \to 0^-} \frac{|-h|}{-h}$

$\Rightarrow f'(0^-) = \lim_{h \to 0^-} \frac{h}{-h} = -1$

So, the left-hand derivative of f(x) = |x| at x = 0 is -1 . This indicates that the function has a negative slope as x approaches 0 from the left side.

Conclusion

As to find the derivative of a function at particular point can make use of One sided derivatives. There will be existence of the derivative of the function at particular point when the limit exists and Left- Hand derivative is equals to the Right Hand derivative.

Read More,

Solved example

Example 1: Verify the following function has left hand derivative and right hand derivative at x=0,

$\bold{y=\begin{cases} x, & x\leq 0\\ 2x, & x > 0 \end {cases}}$

Solution:

For Left hand derivative,

y = f(x) = x

At x=0, f(0) = 0, f(0 + h) = 0 + h = h

Left hand derivative is:

$\begin{aligned} f'(0^-) & =\lim_{h \rightarrow 0^-}\frac{f(0+h)-f(0)}{h}\\ \Rightarrow f'(0^-)&=\lim_{h \rightarrow 0^-}\frac{h-0}{h} \\ \Rightarrow f'(0^-)&=\lim_{h \rightarrow 0^-}\frac{h}{h}\\ \Rightarrow f'(0^-)&=\lim_{h \rightarrow 0^-}(1)=1 \end{aligned}$

For Right hand derivative,

y = f(x) = 2x

At x=0, f(0) = 2(0) =0, and f(0+h) = 2(0) + 2h = 2h

Right hand derivative is,

$\begin{aligned} f'(0^+)&=\lim_{h \rightarrow 0^+}\frac{f(0+h)-f(0)}{h}\\ \Rightarrow f'(0^+)&=\lim_{h \rightarrow 0^+}\frac{2h-0}{h}\\ \Rightarrow f'(0^+)&-=\lim_{h \rightarrow 0^+}\frac{2h}{h}=\lim_{h \rightarrow 0^+}2=2 \end{aligned}$

As Left hand derivative is not equal to right hand derivative,

So, the derivative of y at x=0 Does not exist (or) y is not differentiable at x=0.

Example 2: Show that f'(-3) does not exists if, f(x)= |x+3|+1.

Solution:

Write the given f(x) into piece wise function,

$y=\begin{cases} -(x+3)+1=-x-3+1=-x-2\ , & x\leq -3\\ (x+3)+1=x+3+1=x+4 , & x > -3 \end {cases}$

For Left hand derivative,

y = f(x) = -x-2

At x=-3, f(-3) = -(-3) – 2 = 1, and f(-3+h) = -(-3)-h-2 = 3-h-2 = 1-h

Left hand derivative is,

$\begin{aligned} f'(-3^-)=& \lim_{h \rightarrow 0^-}\frac{f(-3+h)-f(-3)}{h}\\ \Rightarrow f'(-3^-)& =\lim_{h \rightarrow 0^-}\frac{1-h-1}{h}=\lim_{h \rightarrow 0^-}\frac{-h}{h}\\ \Rightarrow f'(-3^-)& =\lim_{h \rightarrow 0^-}(-1)=-1 \end{aligned}$

For Right hand derivative,

y = f(x) = x+4

At x = -3, f(-3) = -3+4 = 1, and

f(-3+h) = h+1

Right hand derivative is,

$\begin{aligned} f'(-3^+)& =\lim_{h \rightarrow 0^+}\frac{f(-3+h)-f(-3)}{h}\\ \Rightarrow f'(-3^+)& =\lim_{h \rightarrow 0^+}\frac{h+1-1}{h}=\lim_{h \rightarrow 0^+}\frac{h}{h}\\ \Rightarrow f'(-3^+)& =\lim_{h \rightarrow 0^+}(1)=1 \end{aligned}$

As Left hand derivative is not equal to right hand derivative,

So, the derivative of y at x=-3 Does not exist (or) y is not differentiable at x=-3.

Practice problems

Problem 1: Verify f(x) is differentiable at x=1,

$f(x)=\begin{cases} x-3, & x\geq 1 \\ x, & x<1 \end{cases}$

Problem 2: Show that f'(-1) does not exist, for,

$f(x)=\begin{cases} x^{2}-4, & x\leq -1 \\ x+3, & x>-1 \end{cases}$