Lami’s Theorem

Lami’s Theorem, also known as Lami’s Law, is a principle in statics and mechanics of materials that relates the forces acting on a body in static equilibrium. It is named after the Italian mathematician and physicist Bernard Lami. Lami’s Theorem is typically applied to a body or structure subjected to concurrent forces. Imagine three friends pulling a string simultaneously from different directions, considering the plane is coplanar. Through the help of Lami’s theorem, one can easily find the forces each friend is exerting.

Further in this article, we will learn about the statement, formula, step-by-step proof, essential assumptions, and practical applications of Lami’s Theorem. Additionally, there will be a few practice problems for better understanding and clarification.

What is Lami’s Theorem?

Lami’s Theorem, named after the 18^th-century Armenian-French mathematician Gabriel Lami; is a principle in static and structural engineering. Lami’s Theorem verifies the equilibrium of the system under concurrent forces.

Lami’s Theorem is particularly useful when analyzing the equilibrium of structures and trusses subjected to concurrent forces. Lami’s Theorem provides a mathematical relationship between the magnitudes and directions of these forces when the system is in static equilibrium.

Statement of Lami’s Theorem

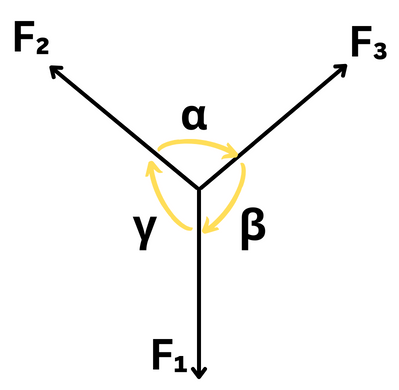
When three coplanar forces act simultaneously at a point, achieving equilibrium among them, each force is proportional to the sine of the angle between the other two forces.

Lami’s Theorem Formula

The theorem states that for a body in static equilibrium if three coplanar forces act on a point and keep it in equilibrium, each force is proportional to the sine of the angle between the other two forces. Mathematically, it can be expressed as:

F₁/sin α= F₂/sin β = F₃/sin γ

Where,

• F₁, F₂, and F₃ are the magnitudes of the forces, and
• α, β, and γ are the angles between the forces.

Assumption in Lami’s Theorem

Certain assumptions need to be followed when using Lami’s Theorem and the assumptions are:

• Forces acting must be within the same plane, that is coplanar.
• These forces are required to converge at a single point, which shows concurrent forces meeting at a common intersection.
• The system should be in a state of static equilibrium, which implies that forces sums to zero and the system is at rest.

By following to these conditions is important for the proper application and practical effectiveness of Lami’s Theorem in real-world scenarios.

Lami’s Theorem Proof

To understand why vectors must balance, imagine three coplanar, concurrent and non-collinear vectors, let’s call them F₁, F₂, F₃ vectors need to add up to zero, symbolized by F₁+F₂+F₃=0. Now we have to rearrange the vectors such that they form a triangle, where the sides of the triangle are represented by vectors a, b, c. The angles in these triangles, which are denoted by α, β, and γ, are related to the vectors.

To find this connection, let’s use a trick involving the law of sines.

Simplifying further, we know that sin(180° – θ)=sin θ

That’s Lami’s Theorem, where the ratio of triangle’s sides to the sines of their opposite angles is equal. In simpler terms, it’s a neat way to understand how forces balance when they’re all pulling or pushing at a common point.

Application of Lami’s Theorem

Lami’s Theorem can analyze concurrent forces in equilibrium, and its practical applications involve structural engineering and physics. Here are some practical applications:

• Mechanical Systems: When dealing with multiple components in a mechanical system, Lami’s Theorem helps understand different forces acting on different elements. This is crucial in designing linkages, levers, and other mechanical systems where forces converge at a specific point.
• Load Distribution in Bridges: Bridges often experience complex force distributions due to the varying loads they bear. Lami’s Theorem helps in assessing the equilibrium of forces at key points in bridge structures, adding strength to the design and safety to the overall system.
• Statics in Physics Education: Lami’s Theorem is generally introduced in physics education to teach students about vector forces and equilibrium. It’s a tool for solving problems related to static systems, and ultimately helping for more advanced concepts in mechanics.

Limitation of Lami’s Theorem

There are some limitation of Lami’s Theorem, these are listed as follows:

• Lami’s theorem applies when all forces act in the same plane and meet at a single point.
• It works when the object is at rest and not undergoing acceleration.
• Forces must be accurately represented as vectors for the theorem to be applied correctly.
• Lami’s theorem assumes the object is rigid and doesn’t deform under the applied forces.
• Material characteristics of the object are not taken into account.
• Specifically designed for systems with exactly three forces meeting at a point.
• The theorem focuses on forces but doesn’t consider moments or couples.
• Applicable only in static (non-accelerating) conditions.

Read More,

• Scalars and Vectors
• Types of Vectors
• Vector Algebra

Solved Problems on Lami’s Theorem for IIT JEE

Problem 1. Consider a cable-stayed bridge where three cables converge at a single point, forming angles α=60°, β=90°, and γ=30° with the horizontal. If the tension in one cable is 800 N, use Lami’s Theorem to find the tensions in the other two cables.

Solution:

Applying Lami’s Theorem:

Solving for T₂ and T₃, we get

T₂ = 800N × ((√3)⁄2) ≈ 692.82N

T₃ = 800N × (1 ⁄2) ≈ 400N

Problem 2: In a mechanical linkage system, three forces F₁ =200N, F₂ = 300N and F₃ = 400N act concurrently at a joint. If the angles between these forces are α=45°, β=60°, and γ=75°, use Lami’s Theorem to find the resultant force at the joint.

Solution:

Applying Lami’s Theorem:

Solving for the resultant force:

Resultant force ≈ 141.42+259.81+400 ≈ 801.23N

Problem 3: A sailing yacht experiences three wind forces F₁ = 500N, F₂ = 600N and F₃ = 800N act concurrently at angles α=30°, β=45°, and γ=60°, with the sail. Determine the total force and its direction, considering Lami’s Theorem.

Solution:

Applying Lami’s Theorem:

Total force= 500 × 2 + 600 × (√2)⁄2 + 800 × (√3)⁄2 ≈ 2298.45N

To find the direction, calculate the angle θ opposite to the resultant force

⇒ θ ≈ 52.6°

Hence, the total force acting is approximately 52.6° with the horizontal.

Practice Problems on Lami’s Theorem

Problem 1: Consider a truss where three forces F₁, F₂, F₃ are applied concurrently at a joint, forming angles α=30°, β=60°, and γ=90° with the horizontal, respectively. The magnitudes of forces are given as follows: F₁ = 500N, F₂ = 600N, F₃ = 800N . Use Lami’s Theorem to find the magnitudes of these forces.

Problem 2: Imagine a bracket subjected to three forces F₁ = 100N, F₂ = 150N and F₃ = 200N, with α=45°, β=45°, and γ=90°. Use Lami’s Theorem to find the tension in each force.

Problem 3: A uniform beam is supported by two cables attached to its ends. If the angles between the cables and the beam are known, determine the tensions in the cables to keep the beam in equilibrium.

Problem 4: A triangular plate is subjected to three forces at its vertices. If the forces are concurrent and in equilibrium, find the magnitude and direction of each force.

Problem 5: Three forces of magnitudes 10 N, 15 N, and 20 N are applied to a point. If the angles between the forces are 30 degrees and 150 degrees, find the resultant force.

Lami’s Theorem: FAQs

1. What is Lami’s Theorem?

Lami’s Theorem is the relation between three coplanar, concurrent and nonlinear forces and their angles.

2. Why is Lami’s Theorem Important?

Its importance is that it provides a simplified method to analyse, and predict the behaviour of forces in various structures, aiding in the design and optimization of mechanical components.

3. What are the Assumptions in Lami’s Theorem?

Lami’s Theorem assumes that the forces are coplanar, concurrent, and the system is in static equilibrium.

4. What is the Mathematical Expression of Lami’s Theorem?

If F₁, F₂, and F₃ are three forces acting on a particle at a point, and θ₁, θ₂, and θ₃ are the angles between the forces, then Lami’s theorem can be expressed as:

5. How many Forces are required for the Lami’s theorem?

Three forces are required for Lami’s Theorem.

6. Can Lami’s Theorem be Applied to any Force System?

No, Lami’s theorem is specifically applicable to coplanar, concurrent force systems with three forces. It is not valid for non-concurrent force systems or systems with more or fewer than three forces.

7. Are there any Limitations to Lami’s Theorem?

Lami’s theorem is limited to three concurrent forces in a coplanar system. Lami’s theorem does not apply to systems with more than three forces or forces acting in three-dimensional space.

8. Can Lami’s Theorem be used for Vectors?

Lami’s theorem is generally used for scalar quantities. However, it can be extended to vectors by applying the principle separately to the components of the vectors in the chosen coordinate system.