Kth largest factor of number N
Last Updated :
28 Nov, 2022
Given two positive integers N and K, the task is to print the Kth largest factor of N.
Input: N = 12, K = 3
Output: 4
Explanation: The factors of 12 are {1, 2, 3, 4, 6, 12}. The largest factor is 12 and the 3rd largest factor is 4.
Input: N = 30, K = 2
Output: 15
Explanation: The factors of 30 are {1, 2, 3, 5, 6, 10, 15, 30} and the 2nd largest factor is 15.
Approach: The idea is to check for each number in the range [N, 1], and print the Kth number that divides N completely.
Iterate through the loop from N to 0. Now, for each number in this loop:
- Check if it divides N or not.
- If N is divisible by the current number, decrement the value of K by 1.
- When K becomes 0, this means that the current number is the Kth largest factor of N.
- Print the answer according to the above observation.
Below is the implementation of the above approach:
C
#include <stdio.h>
int KthLargestFactor(int N, int K)
{
for (int i = N; i > 0; i--) {
if (N % i == 0)
K--;
if (K == 0) {
return i;
}
}
return -1;
}
int main()
{
int N = 12, K = 3;
printf("%d", KthLargestFactor(N, K));
return 0;
}
|
C++
#include <iostream>
using namespace std;
int KthLargestFactor(int N, int K)
{
for (int i = N; i > 0; i--) {
if (N % i == 0)
K--;
if (K == 0) {
return i;
}
}
return -1;
}
int main()
{
int N = 12, K = 3;
cout << KthLargestFactor(N, K);
}
|
Java
import java.io.*;
class GFG {
static int KthLargestFactor(int N, int K)
{
for (int i = N; i > 0; i--) {
if (N % i == 0)
K--;
if (K == 0) {
return i;
}
}
return -1;
}
public static void main(String[] args)
{
int N = 12, K = 3;
System.out.println(KthLargestFactor(N, K));
}
}
|
Python
def KthLargestFactor(N, K):
for i in range(N, 0, -1):
if N % i == 0:
K -= 1
if K == 0:
return i
return -1
N = 12
K = 3
print(KthLargestFactor(N, K))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int KthLargestFactor(int N, int K)
{
for (int i = N; i > 0; i--) {
if (N % i == 0)
K--;
if (K == 0) {
return i;
}
}
return -1;
}
public static void Main()
{
int N = 12, K = 3;
Console.Write(KthLargestFactor(N, K));
}
}
|
Javascript
<script>
function KthLargestFactor(N, K)
{
for (let i = N; i > 0; i--) {
if (N % i == 0)
K--;
if (K == 0) {
return i;
}
}
return -1;
}
let N = 12, K = 3;
document.write(KthLargestFactor(N, K));
</script>
|
Time Complexity: 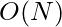
Auxiliary Space: 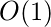
Efficient Approach: The problem can be solved in an optimized way in sqrt(n) complexity by using the fact that factors of any number remain in the form of pairs. In other words, if i is a factor of number n then n/i will also be a factor of n. So in order to find all the factors of the number we need to check for factors till sqrt(n) and their corresponding pairs. A similar type of approach is used in the article: find divisors of natural numbers.
Illustration:
If n = 80, then all the various pairs of divisors possible are: (1,80), (2,40), (4,20), (5,16), (8,10). Hence in order to store all the factors of 80, we will iterate the loop from 1 to √80 ≈ 8 and store the factors in the range(which includes 1,2,4,5,8 here in this case). After this, we run a reverse loop and store the pairs of these previous factors (which will give 10, 16, 20, 40, and 80). Here we are running a reverse loop so that we can get the pairs in increasing order. In this way, we will get all the factors which include {1, 2, 4, 5, 8, 10, 16, 20, 40, and 80}.
Approach:
- Initialize a vector to store the elements in increasing order.
- First, iterate a loop from 1 to sqrt(n) and store all the factors.
- Then iterate the loop in reverse order and for each factor store its corresponding pair. So if i is the factor then store n/i.
- If the size of the vector is greater or equal to k then return the kth largest factor(which will be v[v.size()-k] as the vector v is in increasing order).
- If k elements do not exist that means there is no kth largest factor and hence return -1.
Handling the corner cases:
A corner case will arise when any factor is exactly equal to sqrt(n). For example, if n=100, then in this case 10 will be a factor of the number, and also its corresponding pair is 10 as (10*10=100). So in this case 10 will be taken two times. In order to tackle this case, we use an if statement between two loops and remove the issue by considering this factor only one time.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int KthLargestFactor(int n, int k)
{
vector<int> v;
int i;
for (i = 1; i * i <= n; i++) {
if (n % i == 0)
v.push_back(i);
}
if (i * i == n) {
i--;
}
for (; i >= 1; i--) {
if (n % i == 0)
v.push_back(n / i);
}
if (k <= v.size()) {
return v[v.size() - k];
}
else
return -1;
}
int main()
{
int N = 12, K = 3;
cout << KthLargestFactor(N, K);
}
|
Java
import java.io.*;
import java.util.*;
public class Main
{
static int KthLargestFactor(int n, int k)
{
ArrayList<Integer> v = new ArrayList<Integer>();
int i;
for (i = 1; i * i <= n; i++) {
if (n % i == 0)
v.add(i);
}
if (i * i == n) {
i--;
}
for (; i >= 1; i--) {
if (n % i == 0)
v.add(n / i);
}
if (k <= v.size()) {
return v.get(v.size() - k);
}
else
return -1;
}
public static void main(String[] args)
{
int N = 12, K = 3;
System.out.println(KthLargestFactor(N, K));
}
}
|
Python3
import math
def KthLargestFactor(n, k):
v = []
i = 1
x = math.ceil(math.sqrt(n))
for j in range (1,x):
if (n % j == 0):
v.append(i)
i = j
if (i * i == n):
i-=1
for j in range(i,0,-1):
if (n % i == 0):
v.append(math.floor(n / i))
if (k <= len(v)):
return v[len(v)- k]
else:
return -1
N = 12
K = 3
print(KthLargestFactor(N, K))
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
public class GFG {
static int KthLargestFactor(int n, int k)
{
ArrayList v = new ArrayList();
int i;
for (i = 1; i * i <= n; i++) {
if (n % i == 0)
v.Add(i);
}
if (i * i == n) {
i--;
}
for (; i >= 1; i--) {
if (n % i == 0)
v.Add(n / i);
}
if (k <= v.Count) {
return (int)v[v.Count - k];
}
else
return -1;
}
static public void Main()
{
int N = 12, K = 3;
Console.WriteLine(KthLargestFactor(N, K));
}
}
|
Javascript
function KthLargestFactor(n, k)
{
var v=[];
var i;
for (i = 1; i * i <= n; i++) {
if (n % i == 0)
v.push(i);
}
if (i * i == n) {
i--;
}
for (; i >= 1; i--) {
if (n % i == 0)
v.push(n / i);
}
if (k <= v.length) {
return v[v.length - k];
}
else
return -1;
}
var N = 12;
var K = 3;
console.log(KthLargestFactor(N, K));
|
Time Complexity: O(sqrt(n))
Auxiliary Space: O(m) where m is the total number of factors of n.
Share your thoughts in the comments
Please Login to comment...