Find Multiples of 2 or 3 or 5 less than or equal to N
Last Updated :
31 Aug, 2022
Given an integer 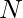 . The task is to count all such numbers that are less than or equal to N which are divisible by any of 2 or 3 or 5.
. The task is to count all such numbers that are less than or equal to N which are divisible by any of 2 or 3 or 5.
Note: If a number less than N is divisible by both 2 or 3, or 3 or 5, or all of 2,3 and 5 then also it should be counted only once.
Examples:
Input : N = 5
Output : 4
Input : N = 10
Output : 8
Simple Approach: A simple approach is to traverse from 1 to N and count multiple of 2, 3, 5 which are less than equal to N. To do this, iterate up to N and just check whether a number is divisible by 2 or 3 or 5. If it is divisible, increment the counter and after reaching N, print the result.
Time Complexity: O(N).
Efficient Approach: An efficient approach is to use the concept of set theory. As we have to find numbers that are divisible by 2 or 3 or 5.

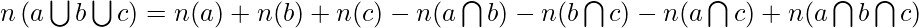
Now the task is to find n(a),n(b),n(c),n(a b), n(b
b), n(b c), n(a
c), n(a c), and n(a
c), and n(a b
b c). All these terms can be calculated using Bit masking. In this problem we have taken three numbers 2,3, and 5. So, the bit mask should be of 2^3 bits i.e 8 to generate all combination of 2,3, and 5.
c). All these terms can be calculated using Bit masking. In this problem we have taken three numbers 2,3, and 5. So, the bit mask should be of 2^3 bits i.e 8 to generate all combination of 2,3, and 5.
Now according to the formula of set union, all terms containing odd numbers of (2,3,5) will add into the result and terms containing even number of (2,3,5) will get subtracted.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countMultiples(int n)
{
int multiple[] = { 2, 3, 5 };
int count = 0, mask = pow(2, 3);
for (int i = 1; i < mask; i++) {
int prod = 1;
for (int j = 0; j < 3; j++) {
if (i & 1 << j)
prod = prod * multiple[j];
}
if (__builtin_popcount(i) % 2 == 1)
count = count + n / prod;
else
count = count - n / prod;
}
return count;
}
int main()
{
int n = 10;
cout << countMultiples(n) << endl;
return 0;
}
|
Java
class GFG{
static int count_setbits(int N)
{
int cnt=0;
while(N>0)
{
cnt+=(N&1);
N=N>>1;
}
return cnt;
}
static int countMultiples(int n)
{
int multiple[] = { 2, 3, 5 };
int count = 0, mask = (int)Math.pow(2, 3);
for (int i = 1; i < mask; i++) {
int prod = 1;
for (int j = 0; j < 3; j++) {
if ((i & 1 << j)>0)
prod = prod * multiple[j];
}
if (count_setbits(i) % 2 == 1)
count = count + n / prod;
else
count = count - n / prod;
}
return count;
}
public static void main(String[] args)
{
int n = 10;
System.out.println(countMultiples(n));
}
}
|
Python 3
def countMultiples( n):
multiple = [ 2, 3, 5 ]
count = 0
mask = int(pow(2, 3))
for i in range(1,mask):
prod = 1
for j in range(3):
if (i & (1 << j)):
prod = prod * multiple[j]
if (bin(i).count('1') % 2 == 1):
count = count + n // prod
else:
count = count - n // prod
return count
if __name__=='__main__':
n = 10
print(countMultiples(n))
|
C#
using System;
public class GFG{
static int count_setbits(int N)
{
int cnt=0;
while(N>0)
{
cnt+=(N&1);
N=N>>1;
}
return cnt;
}
static int countMultiples(int n)
{
int []multiple = { 2, 3, 5 };
int count = 0, mask = (int)Math.Pow(2, 3);
for (int i = 1; i < mask; i++) {
int prod = 1;
for (int j = 0; j < 3; j++) {
if ((i & 1 << j)>0)
prod = prod * multiple[j];
}
if (count_setbits(i) % 2 == 1)
count = count + n / prod;
else
count = count - n / prod;
}
return count;
}
static public void Main (){
int n = 10;
Console.WriteLine(countMultiples(n));
}
}
|
PHP
<?php
function popcount($value)
{
$count = 0;
while($value)
{
$count += ($value & 1);
$value = $value >> 1;
}
return $count;
}
function countMultiples($n)
{
$multiple = array(2, 3, 5);
$count = 0;
$mask = pow(2, 3);
for ($i = 1; $i < $mask; $i++)
{
$prod = 1;
for ($j = 0; $j < 3; $j++)
{
if ($i & 1 << $j)
$prod = $prod * $multiple[$j];
}
if (popcount($i) % 2 == 1)
$count = $count + (int)($n / $prod);
else
$count = $count - (int)($n / $prod);
}
return $count;
}
$n = 10;
echo countMultiples($n);
?>
|
Javascript
<script>
function count_setbits(N)
{
var cnt=0;
while(N>0)
{
cnt+=(N&1);
N=N>>1;
}
return cnt;
}
function countMultiples(n)
{
var multiple = [ 2, 3, 5 ];
var count = 0, mask = parseInt(Math.pow(2, 3));
for (i = 1; i < mask; i++) {
var prod = 1;
for (j = 0; j < 3; j++) {
if ((i & 1 << j)>0)
prod = prod * multiple[j];
}
if (count_setbits(i) % 2 == 1)
count = count + parseInt(n / prod);
else
count = count - parseInt(n / prod);
}
return count;
}
var n = 10;
document.write(countMultiples(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...